介绍

近年来，群体智能优化算法以其灵活性强、鲁棒性强、实现简单等优点被广泛应用于各个领域的优化问题。它们主要通过模拟自然界各种生物的捕食、迁徙等行为来实现，其中包括灰狼优化算法1(GWO)，粒子群优化算法2(PSO)，鲸鱼优化算法3.(WOA)和麻雀优化算法4(SSA)等。优化算法可以有效地提高系统效率，降低能耗，帮助优化者合理利用资源。同时，这种效应随着优化问题规模的增加而变得更加明显。

灰狼优化器(grey wolf optimizer, GWO)是Mirjalili等人在2014年提出的一种群体智能优化算法，它模拟了灰狼捕食猎物的群体行为和领导机制。该算法广泛应用于参数优化5，6，7背包问题8，9、经济调度问题10，11，12、车间调度问题13，14、故障诊断15，16，17、特征选择18，19，20.、图像处理21，22，23它具有参数少、易于实现等特点。然而，在实际的优化项目中，GWO算法存在收敛速度慢、全局搜索能力不足、容易陷入局部最优解等问题，引起了众多学者的关注，并展开了一系列关于灰狼优化算法的研究。文龙等。24提出了一种受粒子群算法启发的改进灰狼优化算法IGWO。该算法增加了控制参数的非线性调整策略和基于个人历史最优位置和全局最优位置的修正位置更新方程。实验结果表明，该算法求解精度高，收敛速度快，适应度函数求值次数少。米塔尔等人。25注意GWO算法在局部搜索和全局搜索之间的适当平衡。他们通过改变参数调整策略提出了mGWO算法。基于基准问题和WSN聚类问题，验证了该算法收敛速度快、卡在局部极小值的机会少。该算法在实际应用中是非常有效的。Gupta等人。26在领导力增强的启发下，提出了灰狼优化算法GLF-GWO。引入Levy-flight搜索机制更新leader，并通过贪婪选择机制增强算法的局部搜索能力。实验结果表明，GLF-GWO算法具有较好的全局搜索能力，避免陷入局部最优。班萨尔等人。27引入逆学习(OBL)来提高传统灰狼优化算法的探索能力。该算法有效地解决了优化停滞问题，保持了较快的收敛速度。实验证明了该算法的有效性。Mirjalili等人。282016年，在传统灰狼优化算法的基础上，整合归档机制和领导者选择机制，提出了多目标灰狼优化算法(MOGWO)。他们对10个多目标基准问题进行了实验，并与基于分解的多目标进化算法和多目标粒子群算法进行了比较。实验结果表明，该算法具有较强的竞争力。Gharehchopogh29利用高斯突变、柯西突变和Levy战斗来提高TSA算法的全局搜索能力。此外，QLGCTSA结合了量子旋转门，增强了局部搜索能力，增加了种群多样性。实验结果表明，QLGCTSA算法优于其他优化算法。QLGCTSA算法对我们的研究工作有很大的帮助。我们还使用了柯西突变和高斯突变。不同之处是:QLGCTSA对所有搜索代理采用突变算子，而CG-GWO对领队狼采用柯西-高斯突变算子。QLGCTSA采用突变算子提高全局搜索能力，CG-GWO采用突变算子增强局部搜索能力，避免陷入局部最优。为了更好地澄清研究差距，我们将上述算法进行了比较，如表所示1．

表1流行算法的总结。
全尺寸工作台

针对灰狼优化算法存在收敛速度慢、易陷入局部最优解的问题，提出了基于柯西-高斯突变和改进搜索策略的灰狼优化算法。主要贡献如下:

  • 我们设计了柯西-高斯变异算子，该算子作用于领头狼。当领导狼趋向于局部最优解时，搜索范围可以扩大。操作者可以有效地提高领导狼的局部发展能力，避免陷入局部最优。

  • 我们提出一种贪婪选择机制30.，其主要功能是避免变异造成的种群高度多样性。贪心选择机制可以保持种群的多样性，保证算法的收敛速度。

  • 我们设计了一个改进的搜索策略，适用于所有灰狼个体。该策略考虑了所有个体的平均位置，可以有效地扩大搜索空间，提高算法的全局搜索能力。

本文的其余部分组织如下:经典灰狼优化器提供了经典GWO的简要概述。在章节中该方法，详细讨论了提出的改进算法CG-GWO。节”实验仿真及结果分析给出了收敛精度、收敛速度、算法性能、算法运行时间等方面的数值实验和讨论，并对实际应用进行了实例分析。本文的结论和未来的工作在“结论及未来工作”。

经典灰狼优化器

灰狼社会等级制度

灰狼种群的社会等级分为四个层次，如图所示。1．第一层叫做α狼，它在狼群中扮演着决策者的角色。狼具有管理能力，对应于GWO中的最优解。第二层和第三层被称为β狼和δ分别对应GWO中的次优解和第三优解。他们主要负责协助α狼在决策上，共同领导和协助其他狼不断接近猎物。第四层叫做ωWolf，表示优化过程中的其他解，并根据的决策更新位置α，β和δ狼31．在算法迭代过程中，各级灰狼个体处于竞争状态。每次迭代后，必须根据每只灰狼与猎物之间的距离重新选出领队狼。

图1
图1

灰狼的社会等级制度。

全尺寸图像

位置更新

的位置更新α，β和δ灰狼种群的数量取决于猎物的位置，如公式(1)。

$$X(t + 1) = X_{p} (t) - A \cdot D$$
（1）

在哪里X(t + 1)\)表示更新后灰太狼的位置，\ \(间p {} (t))代表猎物的位置，一个系数是向量，和D表示灰狼和猎物之间的距离。

$$D = X {p} (t) - X(t)|$$
(2）
$$C = 2 \cdot r_{1}$$
（3）
$$A = $$A \cdot r_{2} - A $$
（4）

在哪里\ \ (X (t))表示灰太狼的当前位置，C是系数向量，α在迭代过程中从2到0线性减少，并且r_ \ (r_ {1}, {2} \)是[0,1]中的随机向量。

根据灰狼的社会等级，ω狼依靠领头狼来更新位置。之间的距离ω狼和每只领头狼的计算公式为(5，最后根据公式确定灰狼个体的运动方向(6)及(7)。

$ $ \左\{\{聚集}开始D_{\α}= | C_ {1} \ cdot间的{α\}- X | \ hfill \ \ D_{\β}= | C_ {2} \ cdot间{\β}- X | \ hfill \ \ D_{\三角洲}= | C_ {3} \ cdot间{\三角洲}- X | \ hfill \ \ \{聚集}结束\ $ $
（5）
$ $ \左\{\{聚集}开始间的{1}=间的{α\}-现代{1}\ cdot D_{α\}\ hfill \ \间的{2}=间{\β}-现代{2}\ cdot D_{β\}\ hfill \ \间{3}=间{\三角洲}-现代{3}\ cdot D_δ}{\ \ hfill \ \ \{聚集}结束\ $ $
（6）
$$X(t + 1) = \frac{{X_{1} + X_{2} + X_{3}}}{3}$$
(7)

在哪里\(X_{\alpha}，X_{\beta}，X_{\delta})表示的位置α，β和δ狼分别X灰太狼目前的位置是独立的吗\(D_{\alpha}，D_{\beta}，D_{\delta})表示灰狼个体与各领头狼之间的距离，和X(t + 1)\)是更新后灰太狼的位置。

算法流程

传统GWO算法的伪代码如图所示。2．

图2
图2

传统GWO算法的伪代码。

全尺寸图像

该方法

Cauchy-Gaussian突变

在传统GWO算法的后期迭代中，灰狼逐渐向α这导致种群局部搜索缺乏多样性，算法容易过早收敛。为了解决上述问题，本文引入柯西-高斯突变算子来提高领导狼的多样性，增强局部搜索能力。每次迭代之后，α，β和δ狼被选择突变。基于贪婪选择机制，对突变位置和初始位置进行了比较。适应度较好的个体被选择进入下一次迭代。Cauchy-Gaussian突变策略的数学定义如下:

$ $ U_{领袖}(t + 1) =间{领袖}\离开[{1 + \ lambda_{1}柯西\离开({0 \σ^{2}}\右)+ \ lambda_{2}高斯\离开({0 \σ^{2}}\右)}\右]$ $
(8)
$ $ \σ= \ exp \离开({\压裂{{f(间{领袖})- f(间的{α\})}}{{| f(间{\α } )|}}} \ 右)$ $
（9）
$$X(t + 1) = \left\{\begin{gathering} U_{leader} (t + 1) f(U_{leader} (t + 1)) \lef (X_{leader}) \hfill \\ X_{leader}否则\hfill \\ \\ end{gathering} \right
（10）

在哪里\(U_{leader} (t + 1)\)代表领头狼突变后的位置，\(间{领袖}\)代表狼群首领的当前位置，\(柯西(0 \σ^ {2})\)是满足柯西分布的随机变量，高斯(0,\ \(σ^ {2})\)是满足高斯分布的随机变量，\ (f(间{领袖})\)表示领导狼的适合度值，\(f(X_{\alpha})\)的适应度值α狼,\ lambda_ \ (\ lambda_ {1}, {2} \)是随迭代次数自适应调整的动态参数。

$$\lambda_{1} = 1 - \frac{{t^{2}}}{{t^{2}}}$$
（１１）
$$\lambda_{2} = \frac{{t^{2}}}{{t^{2}}}$$
(12)

在哪里t表示当前迭代次数，和T表示迭代的最大次数。

改进的搜索策略

传统的GWO算法在搜索过程中参数较少，易于实现。但该算法的全局搜索能力较弱，在某些情况下容易陷入局部最优。本文提出了一种改进的搜索策略，提高了算法的全局搜索能力，扩大了搜索空间。在当前灰太狼个体位置不变的情况下，扩展了全局搜索空间\ \ (X (t))是根据传统的GWO位置更新公式(7)。数学定义如下:

$ $ U (t + 1) = \左\{\{聚集}开始间{兰德}(t) - r_{1} \ * |间{兰德}(t) - 2 \ * r_{2} \乘以X (t) |, r_{5} \通用电气0.5 \ hfill \ \间的{α\}(t) -间{avg} (t) - r_{3} \ *(磅+ r_{4} \ *(乌兰巴托-磅)),r_ {5} < 0.5 \ hfill \ \ \{聚集}结束\ $ $
(13)

在哪里U(t + 1)\)表示通过改进搜索策略后灰狼个体的位置，\ \(间{兰德}(t))表示从种群中随机选择的灰狼个体的位置tth迭代,\ \ (X (t))表示灰太狼个体的当前位置，\(r_{1}，r_{2}，r_{3}，r_{4}，r_{5}\)是[0,1]中的随机向量，\(X_{\alpha} (t)\)表示α狼的当前位置，\ \(间{avg} (t))表示当前迭代中灰狼种群的平均位置，和磅\ \(乌兰巴托)是决策变量的上界和下界。

$ $ X (t + 1) = \左\{\{聚集}开始U (t + 1), f (U (t + 1) le f (X (t))) \ \ hfill \ \ X (t),否则\ hfill \ \ \{聚集}结束\ $ $
（14）

在哪里X(t + 1)\)表示灰狼个体在中的位置\(t + 1)\)th迭代,f(U(t + 1))\)通过改进的搜索策略更新位置后的适应度值，和\ (f (X (t)) \)是当前位置的适应度值。

在改进的搜索策略中，迭代生成的新解是围绕随机解或最优解生成的，这有助于增强灰狼个体之间的搜索和交流。如果探索公式(13)不能提供更好的位置，使用传统的GWO方法来更新灰狼个体的位置。

CG-GWO算法

CG-GWO算法的伪代码如图所示。3.流程图如图1所示。4．

图3
图3

CG-GWO算法的伪代码。

全尺寸图像
图4
图4

CG-GWO算法流程图。

全尺寸图像

实验仿真及结果分析

实验设计

为了验证我们的方法的性能，实验选择了16个基准函数进行仿真实验，其中5个单峰函数(F1-F5)如表所示2，表中6个多模态函数(F6-F11)3.，以及表中所示的5个定维多模态函数(F12-F16)4．单峰函数只有一个全局最优解，没有局部最优解，因此用于测试算法的收敛性和探索能力。多模态函数只有一个全局最优解，其他都是局部最优解。通过多模态函数测试了算法的全局搜索能力和局部寻优能力。固定维多模态函数比较复杂，需要组合多个基本函数来检验算法的稳定性。

表2单峰函数。
全尺寸工作台
表3多模态函数。
全尺寸工作台
表4定维多模态函数。
全尺寸工作台

这项工作进行了两部分的比较实验来测试我们的方法的有效性。一方面，将提出的算法与传统的灰狼优化算法(GWO)、粒子群优化算法(PSO)、鲸鱼优化算法(WOA)、麻雀优化算法(SSA)和农田肥力算法(FFA)等经典优化算法进行了比较。32．另一方面，将所提算法与增强型领导启发型灰狼优化算法(GLF-GWO)、启发型灰狼优化算法(IGWO)和改进型灰狼优化算法(mGWO)等一系列改进算法进行了比较。

本工作的实验均在一台PC (8G内存，903G硬盘，CPU: Intel i7-4790)上使用python 3.6.8环境实现。为了保证实验的公平性，所有算法在每个函数上独立运行30次。填充大小设置为30，最大迭代次数为200。最后得到各基准函数的最优值(Best)、平均值(Ave)、最差值(worst)和标准值(SD)。

实验结果及分析

收敛精度分析

为了验证本文方法对收敛精度的优化效果，在16个基准函数上与GWO、PSO、WOA、SSA、FFA、IGWO、mGWO、GLF-GWO等算法进行了仿真实验。实验结果见表5和6．加粗部分表示比较结果相对较好。

表5经典优化算法的实验结果对比。
全尺寸工作台
表6改进的GWO算法实验结果对比。
全尺寸工作台

如表所示5， CG-GWO算法在各基准函数上的最优值、平均值和最差值的统计量均处于最优水平。实验给定相同的初始种群大小和迭代次数。在基准函数F12上，我们的方法和实验中其他四种经典优化算法都能找到最优值。然而，我们的方法的平均值、最差值和标准差明显更好。相比之下，在基准函数F1、F2、F3、F4、F7、F9、F10上，我们的方法在实验中与其他经典优化算法相比表现出了绝对的优势。所有的统计数据都高出几个数量级。在基准函数F5和F13上，虽然我们的方法效果不是很明显，但在实验中，从所有统计量来看，我们的方法都优于其他四种经典优化算法。在基准函数F6和F8上，CG-GWO算法和WOA算法都找到了最优值，但我们的方法更加集中和稳定。

如表所示6与一系列改进的GWO算法相比，CG-GWO算法在单峰函数上表现出极大的优越性。尤其是在基准函数F1、F2和F3上，实验中最优值、平均值、最差值和标准差都远远优于其他改进的GWO算法。在基准函数F4和F5上也可以明显看出我们方法的稳定性。在多模态函数上，我们的方法在基准函数F6、F7、F8和F10上都能很好地找到理论最优值。同时，实验中各项统计数据均优于其他优化算法。在基准函数F9上，除了传统的GWO算法外，其他改进算法都找到了该函数的最优值。但相比之下，我们的方法显示出更大的优势。在固定维数的多模态函数上，本文方法的优化精度与实验中其他改进算法相当。实验表明，所有优化算法都在基准函数F12上找到了最优值。GLF-GWO算法在平均值和最差值方面也同时表现出同样的优越性。 But in contrast, our approach was more excellent in standard deviation, and the optimization effect of which was more stable. On the benchmark function F13, the GLF-GWO algorithm and the CG-GWO algorithm had also found the optimal value, but our approach showed more significant concentration and stability.

收敛速度分析

通过收敛性能实验，更直观地观察CG-GWO算法的收敛效果和收敛速度，经典优化算法，以及GWO的一系列改进算法。分别绘制了各算法在16个基准函数上的适应度收敛曲线，如图所示。5和6，以迭代次数为横坐标，适应度值为纵坐标。

图5
图5 图5 图5

经典优化算法的收敛曲线比较。

全尺寸图像
图6
图6 图6 图6

改进的GWO算法收敛曲线比较。

全尺寸图像

从图中可以看出。5实验表明，CG-GWO算法的收敛曲线低于其他经典优化算法。对16个基准函数的收敛精度和收敛速度有了显著提高。对于单峰函数，如F1和F4所示，CG-GWO快速收敛到最优值，但SSA在100次迭代后仍未达到最优值。如F2和F3所示，我们的方法在第10次迭代时已经优化到最优值。GWO算法收敛到最优值，直到第50次迭代。相比之下，PSO、WOA、SSA和FFA算法在经过200次迭代后仍未达到最优值，WOA和SSA算法的优化结果与最优值相差较大。从F5可以看出，PSO并没有收敛到最优值。对于多模态函数，如F6所示，经过200次迭代后，GWO和PSO并不趋于收敛。SSA算法在第110次迭代时收敛，但陷入局部最优。WOA和CG-GWO在迭代开始时收敛曲线斜率都很大。 Although our approach had a slower convergence than WOA in the early stage, the convergence speed and accuracy of which were higher than WOA after 40 iterations. The above comparison also fully reflected the global search ability of our approach. As shown in F7–F8, PSO, SSA and FFA did not converge to the optimal value after 200 iterations. As shown in F9–F11, CG-GWO converged to the optimal value faster than other algorithms. For the fixed-dimension multimodal functions, as shown in F12-F16, all optimization algorithms could converge to close to the optimal value. But in contrast, the CG-GWO algorithm converged faster, and the WOA algorithm converges the slowest. The convergence curve of the WOA algorithm tends to stabilize until the 50th iteration.

从图中可以看出。6与传统的GWO算法及一系列改进算法相比，CG-GWO算法已显示出其优越性。在单峰函数F1-F5上，所有算法都能收敛到最优值。但是我们的方法可以更快地收敛到一个平稳值。在多模态函数F6和F7上，经过200次迭代，我们的方法更接近理论最优值，收敛速度也更快。然而，实验中其他改进算法要么没有收敛到稳定值，要么陷入局部最优值。在多模态函数F8、F9、F10和F11上，实验中的所有优化算法也都能收敛到最优值，但我们的方法收敛速度更快。在固定维数的多模态函数F12和F16上，实验中所有算法的收敛速度具有可比性。但该方法的收敛精度较高。同样，在固定维数的多模态函数F13-F15上，我们的方法比实验中其他优化算法收敛到最优值的速度更快。

因此，我们的方法在收敛精度和收敛速度上都优于实验中的其他优化算法，并且其全局搜索能力也得到了显著提高，可以有效避免陷入局部最优值。实验证明了改进思想的有效性，也体现了CG-GWO算法在解决更复杂的优化问题方面的优越性。

算法性能分析

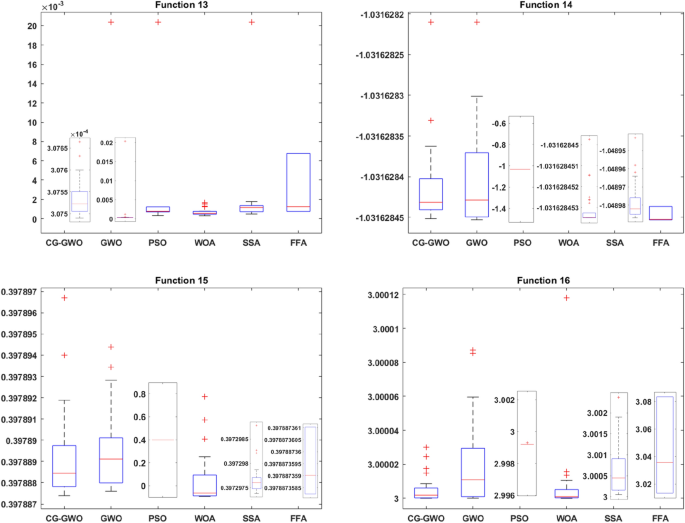
为了评估改进算法的优化能力和稳定性，本文绘制了箱形图33所有算法的16个基准函数。根据箱形图中的上四分、中位数、下四分和异常值进行比较分析。这项工作对所有算法进行了30次独立实验。由于不同算法的实验结果差异较大，因此在绘制箱形图时采用不同的坐标系进行比较，以便更直观地观察比较结果。实验结果如图2所示。7和8．

图7
图7 图7 图7

经典优化算法的箱线图比较。

全尺寸图像
图8
图8 图8 图8

改进GWO算法的箱线图比较。

全尺寸图像

从图中可以看出。7CG-GWO算法在优化过程中分散性较弱，优化值较为集中。在单峰函数F1-F5上，我们的方法优化结果的数量级远小于实验中其他经典优化算法。实验结果表明，改进算法在优化精度和稳定性方面具有优势。在多模态函数F6-F11上，我们的方法比实验中其他经典优化算法更集中，离群值更少。实验结果验证了该方法在全局搜索能力方面的鲁棒性。在固定维数的多模态函数F12-F13上，CG-GWO算法与GWO算法的优化效果相似。在实验中，它们远远优于其他经典的优化算法。然而，我们的方法有更少的异常值，更集中的优化值和更好的优化结果。从F14-F16可以看出，CG-GWO的异常值更少，稳定性更强。

如图所示。8，大多数改进的GWO算法与传统的GWO算法相比具有优势。在单峰函数F1-F5上，CG-GWO算法具有较好的优化效果。在基准函数F3和F5上，各算法的对比程度比较接近，但我们的方法收敛稳定性较高，离群值较少。在多模态函数F6-F11上，只有GLF-GWO算法的优越性与我们的方法接近。虽然由于Levy-flight搜索机制，增强了GLF-GWO算法的全局搜索能力，但也产生了更多的离群值。在固定维数的多模态函数F12-F16上，GLF-GWO算法与我们的方法较为接近。在最优值变化范围上，GLF-GWO算法优于CG-GWO算法，但我们的方法的异常值要少得多。实验结果表明，该方法具有较好的全局搜索能力和较高的稳定性。

算法运行时分析

为了验证CG-GWO算法的计算有效性，本文将CG-GWO算法与其他算法的运行时间进行了比较。实验结果见表7．为节省空间，本文选取了四个具有代表性的函数来绘制柱状图。实验结果如图1所示。9．

表7算法运行时间实验结果对比。
全尺寸工作台
图9
图9

算法的运行时比较。

全尺寸图像

如表所示7和无花果。9改进后的CG-GWO算法存在柯西-高斯突变，耗时较长。在F3、F8和F10中，CG-GWO的运行时间仅低于GLF-GWO。然而，我们可以看到，时间消耗的增加并不是很大。在实际应用中，我们可以接受这种变化。在F12中，CG-GWO的运行时间为medium。因此，CG-GWO算法具有一定的计算有效性。

因此，与经典优化算法和一系列改进的GWO算法相比，CG-GWO算法具有更稳定的收敛能力。该方法在优化精度和离散度方面具有优势。实验结果表明，该方法具有较好的优化能力和稳定的性能。

实际应用案例研究

在本节中，对PSO、WOA、SSA、FFA、GWO、I-GWO、m-GWO、GLF-GWO和CG-GWO这九种算法在工程实际应用中的性能进行了评价:压力容器设计34．

压力容器通常是球形或圆柱形的。圆柱形容器可以垂直或水平定向。垂直容器有很多用途:分馏塔、接触塔、反应器和垂直分离器。这个问题的目的是为了降低圆柱形压力容器两端用半球形封头加固的材料、成型和焊接的总成本，如图所示。10．压力容器设计的数学公式如下:

$ ${聚集}\ \开始分钟f (T_{},识别T_ {h},识别R, L) = 0.6224 T_{年代}RL识别+ 1.7781 T_ {h}识别R ^ {2} + 3.1661 T_{年代}识别^ {2}L + 19.84 T_ {h}识别^ {2}L \ hfill左\ \酸处理\ \{\{聚集}开始g_ {1} = - T_{年代}识别le 0 + 0.0193 R \ \ hfill \ \ g_ {2} = - T_ {h}识别le 0 + 0.0095 R \ \ hfill \ \ g_{3} = - \πR ^ {2} L - 4/3 \πR ^ {3} le 0 + 1296000 \ \ hfill \ \ g_ {4} = le 0 L - 240 \ \ hfill \ \ \{聚集}\正确的结束。\hfill \\ \end{已收集}$$
（15）

在哪里\(0 \le T_{s}，T_{h} \le 99\)和\(10 \ \ R,L \le 200 \)

图10
图10

压力容器设计问题。

全尺寸图像

压力容器的设计问题是最常见的问题之一。研究人员在许多研究中使用优化问题来证实他们的新优化算法的有效性。CG-GWO算法与上述其他算法对压力容器设计问题的最优结果比较如表所示8．根据所得的成本计算结果，对压力容器的设计问题进行了分析8， CG-GWO报最低5884.6849点。优选参数分别为0.779216、0.396459、40.265625、200.000000。

表8压力容器设计问题的优化结果。
全尺寸工作台

压力容器设计问题50次独立运行的统计结果对比见表9．从结果可以看出，CG-GWO的稳定性较好，在Ave和Std值上均表现出优异的效果。

表9 CG-GWO等优化算法对压力容器设计问题的统计结果。
全尺寸工作台

结论及未来工作

针对传统灰狼优化算法收敛速度慢、易陷入局部最优的问题，提出了CG-GWO算法。引入柯西-高斯变异算子，作用于领头狼。根据当前迭代周期动态调整算法中的柯西突变和高斯突变的优势度，提高算法的全局搜索能力。同时，加入贪心机制对导狼进行柯西-高斯突变。保留突变过程中的优秀个体，避免了算法的高度多样性，保证了算法的收敛速度。CG-GWO增加了改进的搜索策略，避免了算法陷入局部最优，提高了算法的收敛精度。在改进的策略中，新解是围绕随机解或最优解生成的。实验结果表明，该方法有效地提高了算法的精度和收敛速度。在精度实验中，CG-GWO显示出数倍的优越性。该算法的收敛性能也能够较快地收敛到最优值，同时箱形图也表明该算法的稳定性较高。 Although CG-GWO did not have much advantage in terms of runtime, the superiority of the algorithm was also demonstrated by the comparison of the pressure vessel design problem.CG-GWO was able to find the optimal value more consistently than other algorithms mentioned in the paper. In conclusion, CG-GWO showed good optimization ability and stability on unimodal functions, multimodal functions, and fixed-dimension multimodal functions, which could effectively avoid falling into the local optimum and expand the individual search space.

虽然CG-GWO算法在大多数情况下具有良好的收敛精度、收敛速度和稳定性，但在某些特定情况下稳定性略差。同时，Cauchy-Gaussian突变将花费更多的时间，这也是该算法运行时间较长的一个局限性。该算法在实际应用中存在一定的局限性。如果问题的规模太大，计算的\ \(间{avg} (t))改进后的搜索策略相对来说比较复杂，这会影响算法的优化进度。另外，如果实际问题中的多个变量相互影响，则很难对领导狼进行选择，并确定变量σ\ (\ \)在柯西-高斯突变中会变得复杂，这也给所提出的算法带来了很大的挑战。在今后的工作中，要注意算法的稳定性提高，提高算法的效率。CG-GWO算法将应用于更复杂的实际工程优化问题，帮助优化者更快、更准确地确定最终的优化方案。