介绍gydF4y2Ba

非线性动力系统都进行了广泛的研究在上个世纪,因此各种各样的方法已经开发出来。介绍性的书籍和现代评论可以发现:参电路分析和控制系统。gydF4y2Ba1gydF4y2Ba,gydF4y2Ba2gydF4y2Ba,gydF4y2Ba3gydF4y2Ba,gydF4y2Ba4gydF4y2Ba,gydF4y2Ba5gydF4y2Ba,gydF4y2Ba6gydF4y2Ba,gydF4y2Ba7gydF4y2Ba;在参考文献结构动力学和振动。gydF4y2Ba8gydF4y2Ba,gydF4y2Ba9gydF4y2Ba,gydF4y2Ba10gydF4y2Ba,gydF4y2Ba11gydF4y2Ba,gydF4y2Ba12gydF4y2Ba;电化学在参考文献。gydF4y2Ba13gydF4y2Ba,gydF4y2Ba14gydF4y2Ba,gydF4y2Ba15gydF4y2Ba,gydF4y2Ba16gydF4y2Ba,gydF4y2Ba17gydF4y2Ba参、普通物理、应用数学。gydF4y2Ba18gydF4y2Ba,gydF4y2Ba19gydF4y2Ba,gydF4y2Ba20.gydF4y2Ba,gydF4y2Ba21gydF4y2Ba,gydF4y2Ba22gydF4y2Ba,gydF4y2Ba23gydF4y2Ba,gydF4y2Ba24gydF4y2Ba。也许,非线性系统的早期研究沃尔泰拉级数gydF4y2Ba25gydF4y2Ba,gydF4y2Ba26gydF4y2Ba在1890年代和维纳系列gydF4y2Ba27gydF4y2Ba,gydF4y2Ba28gydF4y2Ba在1950年代和1940年代。同时,庞加莱的贡献gydF4y2Ba29日gydF4y2Ba在1890年代,范德堡尔gydF4y2Ba30.gydF4y2Ba,LienardgydF4y2Ba31日gydF4y2Ba和费托gydF4y2Ba32gydF4y2Ba在1920年代,Bogolyubov克雷和MitropolskiigydF4y2Ba33gydF4y2Ba,gydF4y2Ba34gydF4y2Ba,gydF4y2Ba35gydF4y2Ba,gydF4y2Ba36gydF4y2Ba在1940年代和1930年代对非线性系统导致了平均的标准理论和微扰方法,谐波平衡法(HBM)和描述函数(DFs)gydF4y2Ba37gydF4y2Ba。这些方法的实际实现的发展gydF4y2BangydF4y2BaonlineargydF4y2Ba一个gydF4y2BautogydF4y2BargydF4y2Ba外呼的gydF4y2Ba米gydF4y2Ba机汇gydF4y2Ba一个gydF4y2Baverage模型与egydF4y2BaxgydF4y2Baogenous输入(NARMAX模型)gydF4y2Ba38gydF4y2Ba,gydF4y2Ba39gydF4y2Ba在1980年代,和汉默斯坦维纳模型,模型和Wiener-Hammerstein模型在2000年代(见参考。gydF4y2Ba40gydF4y2Ba和引用)。gydF4y2Ba

基于谐波分析的傅里叶分析是一种强大的工具,让我们研究一个时域问题的频域表示。线性微分方程可以通过统一的研究框架,如传递函数(TF)的电气和电子工程、频率响应函数(降维)在机械工程和物理中的格林函数。这些框架允许我们计算所有可能的线性行为在频域通过使用第一次谐波。然而,非线性微分方程存在高次谐波,无法避免。许多方法已经发展为了包括更高的谐波,如:广义频率响应函数(导出)gydF4y2Ba41gydF4y2Ba在1950年代;增量谐波平衡科学院水生生物研究所(IHB)gydF4y2Ba42gydF4y2Ba,gydF4y2Ba43gydF4y2Ba,gydF4y2Ba44gydF4y2Ba,gydF4y2Ba45gydF4y2Ba,交替频率/时域方法(尾)gydF4y2Ba46gydF4y2Ba和高阶频率响应函数(HOFRFs)gydF4y2Ba47gydF4y2Ba在1980年代;非线性输出频率响应函数(NOFRF)gydF4y2Ba48gydF4y2Ba,输出频率响应函数(OFRF)gydF4y2Ba49gydF4y2Ba,gydF4y2Ba50gydF4y2Ba,gydF4y2Ba51gydF4y2Ba,高阶正弦输入描述函数(HOSIDFs)gydF4y2Ba52gydF4y2Ba和许多HBM和水生生物研究所的修改版本gydF4y2Ba53gydF4y2Ba,gydF4y2Ba54gydF4y2Ba,gydF4y2Ba55gydF4y2Ba,gydF4y2Ba56gydF4y2Ba,gydF4y2Ba57gydF4y2Ba,gydF4y2Ba58gydF4y2Ba,gydF4y2Ba59gydF4y2Ba在1990年代,2000年代和2010年代。gydF4y2Ba

现代的评论这些方法可以在参考文献中找到。gydF4y2Ba60gydF4y2Ba,gydF4y2Ba61年gydF4y2Ba,gydF4y2Ba62年gydF4y2Ba,gydF4y2Ba63年gydF4y2Ba,gydF4y2Ba64年gydF4y2Ba。根据裁判。gydF4y2Ba60gydF4y2Ba,频域分析的最终目标是“提供一个清晰明确的关系系统输出谱和非线性特征参数”。在这个方向,OFRF方法提供了我们一个明确的关系,但是,需要一个递归算法,以获得这些系数gydF4y2Ba51gydF4y2Ba。此外,HOSIDFs方法引入了一个“虚拟谐波发生器”,可能无意中伪装傅里叶谱之间的关系和非线性系统的物理参数。gydF4y2Ba

这个工作是一个贡献为了定义一个统一的框架与所有的高次谐波非线性系统的物理参数,避免递归算法和虚拟发电机。我们感兴趣的是解决这些问题:我们如何获得尽可能多的信息关于非线性系统的谐波?;之间的关系,更具体地说,系统中的谐波和解析表达式定义方程的非线性系统?gydF4y2Ba

为了解决这些问题,我们提出一个形式是基于傅里叶分析从电气和电子工程的角度gydF4y2Ba65年gydF4y2Ba,gydF4y2Ba66年gydF4y2Ba,gydF4y2Ba67年gydF4y2Ba,gydF4y2Ba68年gydF4y2Ba的目标,但也被应用到其它领域作为一个多学科的工具。“谐波”这个词在这里指的是傅里叶谱获得了快速傅里叶变换(FFT)的连续变量采样。这种形式主义的动机存在的参考书目,主要由OFRF和HOSIDFs方法,但最好的作者的知识,它是新概念。我们认为再形成的傅里叶级数的幂级数表达式,结果,我们发现解析表达式清楚地表明之间的关系的证据傅里叶分析和特性曲线的一阶系统。这些解析表达式可以应用于系统建模和模拟输入-输出数据不使用递归算法或虚拟发电机。这种形式主义意味着通过计算傅里叶谱的驱动力与一个固定的正弦动态变量,我们可以获得一个完整的描述非线性系统的特性曲线。此外,这项工作所示,这些表达式显示之间的等价傅里叶分析和两个多项式配件基于多项式扩展特性曲线。总之,这项工作的目标是启动系统研究的主题确定非线性特性曲线的傅里叶分析,这里的起点要解决是一阶系统。gydF4y2Ba

从技术上讲,这个工作的表达式是基于重写的傅里叶级数的驱动力gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)到一个方便的幂级数表达式的动态变量gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)。这些表达式有一个功能的依赖,可以确定为一阶系统gydF4y2Ba\ (y (t) = f (x (t)) + g (x (t)) x (t) \)gydF4y2Ba。通过使用这些表达式,系统的模型,定义的gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba所谓函数特性曲线,可以得到一个正弦动态变量gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,模型参数的傅里叶系数的驱动力,和的值gydF4y2Ba\ (A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba和gydF4y2Ba\(“_1 =ωA_1 \ \)gydF4y2Ba。驱动力的傅里叶分析给定的顺序gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba让我们获得特性曲线,在范围内gydF4y2Ba\ (x \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba,特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba是由一个多项式扩张订单gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba和gydF4y2Ba\ (k_{马克斯}1 \)gydF4y2Ba,分别。我们证明这个等价之间的傅里叶分析的驱动力和特性曲线的多项式扩展之间实际上是一个等价的傅里叶分析驱动力和特性曲线的多项式曲线配件。由于这种等价,注意到动态变量是输入在建模阶段,提出的方法被称为:“正弦输入反应幂级数(sirp)”。gydF4y2Ba

一旦系统估计的傅里叶分析正弦响应,我们获得的特性曲线可用于时域模拟在两个方面:(1)通过计算对应于一个给动态变量的驱动力;(2)通过计算动态变量,对应于一个驱动力。最后,该方法可以被视为一种结合时频方法,因为系统评估是基于频域法和基于时域仿真法。gydF4y2Ba

结果gydF4y2Ba

形式主义gydF4y2Ba

我们感兴趣的是非线性动力系统建模的一阶方程gydF4y2Ba

$ $ \{对齐}开始y (t) = f (x (t)) + g (x (t)) \;x (t) \{对齐}$ $gydF4y2Ba
(1)gydF4y2Ba

在哪里gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)是动力系统和变量gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)是一种动力,他们将被称为系统的输入和响应,分别。此外,gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba是非线性动力学变量的函数。在电路理论中,gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba函数被称为特性曲线,因为他们描述这个系统。如果这些曲线是已知的,那么情商。gydF4y2Ba1gydF4y2Ba)可以通过使用一些数值技术解决或直接集成。注意,左边有显式的依赖独立变量gydF4y2BatgydF4y2Ba,但右侧不会,因为它依赖于动态变量及其一阶导数。中更详细地讨论这一点gydF4y2Ba应用程序gydF4y2Ba部分阐明的非线性系统可以用情商。gydF4y2Ba1gydF4y2Ba)。gydF4y2Ba

假设gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)是一个周期函数gydF4y2BaTgydF4y2Ba满足狄利克雷条件gydF4y2Ba69年gydF4y2Ba为傅里叶级数的存在,看到裁判。gydF4y2Ba65年gydF4y2Ba现代博览会的主题gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)可以表示为一个傅里叶级数gydF4y2Ba

$ $ \{对齐}开始y (t) = a_0 + \总和_ {k = 1} ^ \ infty (a_k \ cos (k \ωt) + b_k \罪(k \ωt)), \{对齐}$ $gydF4y2Ba
(2)gydF4y2Ba

在哪里gydF4y2Ba\ \(ω= 2 \π/ T \)gydF4y2Ba是基频和傅里叶系数计算了吗gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}{\左\{\开始{数组}{你}和{},a_0 = \压裂{\ω}{\π}\ int _{0} ^{2ω\π/ \}y (t) dt \ \ a_k &{} = \压裂{\ω}{2π\}\ int _{0} ^{2ω\π/ \}y (t) \ cos (k \ωt) dt, \, k \通用电气1 \ \ b_k &{} = \压裂{\ω}{2π\}\ int _{0} ^{2ω\π/ \}y (t) \罪(k \ωt) dt, k \通用电气1。数组{}\ \端。}\{对齐}结束\{对齐}$ $gydF4y2Ba
(3)gydF4y2Ba

通过使用多角度公式gydF4y2Ba

$ ${对齐}\ \开始罪(kx) & = \压裂{e ^ {ikx} - e ^ {ikx}}{2} = \压裂{(\ cos (x) + i \ sin (x)) ^ k - (\ cos (x) - i \ sin (x)) ^ k}{2我}\ nonumber \ \ & = \总和_ {l = 0} ^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\ l (x)因为^ \罪^ {k-l} (x)罪\ \离开(\压裂{\π}{2}(k-l) \) \{对齐}$ $gydF4y2Ba
(4)gydF4y2Ba

和gydF4y2Ba

$ ${对齐}\ \开始cos (kx) & = \压裂{e ^ {ikx} + e ^ {ikx}}{2} = \总和_ {l = 0} ^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\ l (x)因为^ \罪^ {k-l} (x) \因为\离开(\压裂{\π}{2}(k-l) \) \{对齐}$ $gydF4y2Ba
(5)gydF4y2Ba

欧拉公式和二项式定理,然后呢gydF4y2Ba\(\左({\{数组}{c}开始结束k l \ \ \{数组}}\)\)gydF4y2Ba二项式系数,那么我们可以把情商。gydF4y2Ba2gydF4y2Ba),gydF4y2Ba

$ $ \{对齐}开始y (t) = a_0 + \总和_ {k = 1} ^ \ infty \总和_ {l = 0} ^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\因为l罪(\ωt) \ ^ ^ {k-l}(\ωt) (ab) _ {kl} \{对齐}$ $gydF4y2Ba
(6)gydF4y2Ba

在哪里gydF4y2Ba

$ $ \{对齐}开始(ab) _ {kl} {: =} a_k \因为\离开(\压裂{\π}{2}(k-l) \右)+ b_k \罪\离开(\压裂{\π}{2}(k-l) \) \{对齐}$ $gydF4y2Ba
(7)gydF4y2Ba

包含了傅里叶系数gydF4y2Ba\ (a_k \)gydF4y2Ba和gydF4y2Ba\ (b_k \)gydF4y2Ba。进一步的操作可以通过使用毕达哥拉斯的身份gydF4y2Ba\ \ (sin (x) ^ 2 + \ cos (x) = 1 ^ 2 \)gydF4y2Ba。我们使用表达式gydF4y2Ba

$ ${对齐}\ \开始因为^ l(\ωt) ={\左\{{数组}{你}\ \开始离开(1 - \罪^ 2(\ωt) \右)^ {l / 2}和{}\文本{如果l甚至}\ \ \因为^ {l - 1}(\ωt) \ cos(\ωt) &{}{如果l是奇数}\ \文本数组{}\正确的结束。}={\左\{{数组}{你}\ \开始离开(1 - \罪^ 2(\ωt) \右)^ {l / 2}和{}\文本{如果l甚至}\ \ \离开(1 - \罪^ 2(\ωt) \右)^ {(l - 1) / 2} \ cos(\ωt) &{}{如果l是奇数}\ \文本数组{}\正确的结束。}\{对齐}$ $gydF4y2Ba
(8)gydF4y2Ba

重写情商。gydF4y2Ba6gydF4y2Ba)gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}左y (t) & = \ [+ \, a_0和_ {k = 1} ^ \ infty \总和_{\{数组}}{c l = 0开始结束\ \ l = l + 2 \{数组}}^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开(1 - \罪^ 2(\ωt) \右)^ {l / 2} \罪^ {k-l}(\ωt) (ab) _ {kl} \] \ \ &左\四+ \[\总和_ {k = 1} ^ \ infty \总和_{\{数组}{c}开始l = 1 \ \ l = l + 2 \{数组}}结束^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开(1 - \罪^ 2(\ωt) \右)^ {(l - 1) / 2} \罪^ {k-l}(\ωt) (ab) _ {kl} \] \ cos(\ωt)。结束\{对齐}\{对齐}$ $gydF4y2Ba
(9)gydF4y2Ba

注意,根据情商。gydF4y2Ba6gydF4y2Ba和通过情商的表达式。gydF4y2Ba8gydF4y2Ba),没有其他方法写情商。gydF4y2Ba9gydF4y2Ba),即没有别的方法写一个只包含的术语gydF4y2Ba\ \ (sin(\ωt) \)gydF4y2Ba它包含和其他术语gydF4y2Ba\ \ (sin(\ωt) \)gydF4y2Ba,乘以gydF4y2Ba\ \因为(\ωt) \)gydF4y2Ba。最后一次操作可以将括号表达式转换为力量的总和gydF4y2Ba\罪(\ \)gydF4y2Ba功能,通过使用二项展开式得到gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}左y (t) & = \ [+ \, a_0和_ {k = 1} ^ \ infty \总和_{\{数组}}{c l = 0开始结束\ \ l = l + 2 \{数组}}^ k \总和_ {m = 0} ^ {l / 2} \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开({\{数组}{c}开始结束l / 2 \ \ \{数组}}\右)(1)^ m \罪^ {2 m + k-l}(\ωt) (ab) _ {kl} \] \ \ &左\四+ \[\总和_ {k = 1} ^ \ infty \总和_{\{数组}{c}开始l = 1 \ \ l = l + 2 \{数组}}结束^ k \总和_ {m = 0} ^ {(l - 1) / 2} \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开({\开始{数组}{c} (l - 1) / 2 \ \ m \结束{数组}}\右)(1)^ m \罪^ {2 m + k-l}(\ωt) (ab) _ {kl} \] \ cos(\ωt)。结束\{对齐}\{对齐}$ $gydF4y2Ba
(10)gydF4y2Ba

它只取决于我们得到一个表达式gydF4y2Ba\ \因为(\ωt) \)gydF4y2Ba和的力量gydF4y2Ba\ \ (sin(\ωt) \)gydF4y2Ba。现在考虑一个变量变化gydF4y2Ba\ \ (sin(\ωt) \)gydF4y2Ba来gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2Ba\ \ (x (t) ! = \ !一个_1\sin (\omega t)+A_0\),gydF4y2BaR \ (A_0 \ \ mathbb {} \)gydF4y2Ba,gydF4y2Ba\ (A_1 > 0 \)gydF4y2Ba,gydF4y2Ba在[0,2 \ \ (t \π/ω\]\)gydF4y2Ba。它的导数是gydF4y2Ba\ \ (x (t) ! = \ !一个_1\omega \cos (\omega t)\)。通过定义大小gydF4y2Ba

$ ${对齐}“_1 \开始{:=}和{马克斯}\文本(x ' (t)) = A_1ω\ \{对齐}$ $gydF4y2Ba
(11)gydF4y2Ba

在哪里gydF4y2Ba\(文本\{马克斯}\)gydF4y2Ba是最大的函数。最后,情商。gydF4y2Ba10gydF4y2Ba可以转换成)gydF4y2Ba

$ $ \{对齐}开始y (t) & = \ underbrace{\离开[a_0 + \总和_ {k = 1} ^ \ infty \总和_{\{数组}}{c l = 0开始结束\ \ l = l + 2 \{数组}}^ k \总和_ {m = 0} ^ {l / 2} \离开({\{数组}}{c k开始\ \ l \结束{数组}}\)\离开({\{数组}{c}开始结束l / 2 \ \ \{数组}}\右)(1)^ m \离开(\压裂{x (t) a_0} {A_1} \右)^ {2 m + k-l} (ab) _ {kl} \]} _ {{: =} F \离开(\压裂{x (t) a_0} {A_1} \右)}\ nonumber \ \ & \四+ \ underbrace{左\[\总和_ {k = 1} ^ \ infty \总和_{\{数组}{c}开始l = 1 \ \ l = l + 2 \{数组}}结束^ k \总和_ {m = 0} ^ {(l - 1) / 2} \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开({\开始{数组}{c} (l - 1) / 2 \ \ m \结束{数组}}\右)(1)^ m \离开(\压裂{x (t) a_0} {A_1} \右)^ {2 m + k-l} (ab) _ {kl} \]} _ {{: =} G \离开(\压裂{x (t) a_0} {A_1} \右)}左(\ \压裂{x (t)} {A_1 '} \右)\{对齐}$ $gydF4y2Ba
(12)gydF4y2Ba

的功能gydF4y2BaFgydF4y2Ba和gydF4y2BaGgydF4y2Ba被定义为进一步参考。情商的功能依赖。gydF4y2Ba12gydF4y2Ba)类似于一阶系统中定义的情商。gydF4y2Ba1gydF4y2Ba),我们确认gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}F \ !左(\ \压裂{x (t) a_0} {A_1} \右)& = f (x (t)) \ \ \ !左(\ \压裂{x (t) a_0} {A_1} \) \压裂{1}{A_1 '} & = g (x (t))。结束\{对齐}\{对齐}$ $gydF4y2Ba
(13)gydF4y2Ba

这个方程式之间的关系。(gydF4y2Ba1gydF4y2Ba)和(gydF4y2Ba12gydF4y2Ba)可以被记住的唯一性证明情商。gydF4y2Ba9gydF4y2Ba),因此,情商的独特性。gydF4y2Ba12gydF4y2Ba)。这种独特性使我们能够匹配方程式。(gydF4y2Ba1gydF4y2Ba)和(gydF4y2Ba12gydF4y2Ba)基于相同的函数依赖,产生情商。gydF4y2Ba13gydF4y2Ba)。如果我们强迫动态变量满足gydF4y2Ba\ \ (x (t) ! = \ !一个_1\sin (\omega t)+A_0\),我们可以计算的傅里叶分析gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)获得特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba。方程(gydF4y2Ba12gydF4y2Ba)取决于gydF4y2Ba\ (A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba,gydF4y2Ba\ (a_0 \)gydF4y2Ba和gydF4y2Ba\ ((ab) _ {kl} \)gydF4y2Ba,最后两个的傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)gydF4y2Ba\ \ (x (t) ! = \ !一个_1\sin (\omega t)+A_0\)根据情商。gydF4y2Ba7gydF4y2Ba)。为了更明确的依赖特性曲线的参数形式,我们定义一组gydF4y2Ba\ \ {a_k, b_k \} \)gydF4y2Ba的傅里叶系数,然后,特性曲线取决于参数gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}f (x (t)) & = f (x (t); \ {a_k, b_k \}, A_0, A_1) \ \ g (x (t)) & = g (x (t); \ {a_k, b_k \}, A_0, A_1, A_1”)。结束\{对齐}\{对齐}$ $gydF4y2Ba
(14)gydF4y2Ba

总之,获得系统建模的过程包括傅里叶系数的计算gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)一个正弦动态变量gydF4y2Ba\ \ (x (t) ! = \ !一个_1\sin (\omega t)+A_0\)那么,用情商。gydF4y2Ba13gydF4y2Ba),我们评估gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba特性曲线的基础上,定义从方程式。(gydF4y2Ba12gydF4y2Ba)和(gydF4y2Ba13gydF4y2Ba),最后,我们可以绘制特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba代表系统。然后,系统仿真,我们使用这些特性曲线时域仿真。重要的是要注意,这些模拟的参数gydF4y2Ba\ (A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba,gydF4y2Ba\ (a_0 \)gydF4y2Ba和gydF4y2Ba\ ((ab) _ {kl} \)gydF4y2Ba保持固定的值之前估计的正弦响应。自从特性曲线定义的系统,我们可以计算的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba对应于其他动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba通过一个简单的评估方面的情商。gydF4y2Ba12gydF4y2Ba)。同样,我们可以计算动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba对应于给定的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba直接集成的情商。gydF4y2Ba12gydF4y2Ba)。gydF4y2Ba

值得指出的是一些评论:gydF4y2Ba

  • 上面解释的过程并不是实际的实际实现的方法,因为有计算上更便宜的替代品情商。gydF4y2Ba12gydF4y2Ba)。实际的过程提出了gydF4y2Ba实现gydF4y2Ba部分。gydF4y2Ba

  • 我们认为是一个动态变量gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,但一个函数的系统建模也是有效的一个阶段gydF4y2Ba\ (x (t) = A_1 \罪(\ \φωt +) + A_0 \)gydF4y2Ba。在这种情况下,转换gydF4y2Ba\ (t_{新}= t +识别\φω/ \ \)gydF4y2Ba动态变量和驱动力允许我们使用情商。gydF4y2Ba12gydF4y2Ba)。gydF4y2Ba

傅里叶分析和特性曲线gydF4y2Ba

之前gydF4y2Ba实现gydF4y2Ba节中,重要的是分析情商的条款。gydF4y2Ba12gydF4y2Ba详细)。在本节的其余部分,我们发现显式表达式显示之间的等价的傅里叶分析和特性曲线的多项式回归。为了方便的符号,我们定义gydF4y2Ba

$ $ \{对齐}开始z (t) &{: =} \压裂{x (t) a_0} {A_1}。\{对齐}$ $gydF4y2Ba
(15)gydF4y2Ba

通过重组与情商同样的权力。gydF4y2Ba12gydF4y2Ba),它可以找到泰勒展开式gydF4y2BaFgydF4y2Ba和gydF4y2BaGgydF4y2Ba,即gydF4y2Ba

$ $ \{对齐}开始F (z (t)) & = \总和_ {j = 0} ^ {\ infty} f_j (z (t)) ^{对齐}$ $ j \结束gydF4y2Ba
(16)gydF4y2Ba
$ $ \{对齐}开始G (z (t)) & = \总和_ {j = 0} ^ {\ infty} g_j (z (t)) ^{对齐}$ $ j \结束gydF4y2Ba
(17)gydF4y2Ba

在哪里gydF4y2Ba

$ ${对齐}f_j& = \ \开始和_{\{数组}{c}开始k =结束j k = k + 2 \ \ \{数组}}^ \ infty左(ab) _ {kj} \[\总和_{\{数组}{c}开始l = k-j \ \ l = l + 2 \{数组}}结束^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开({\{数组}{c}开始l / 2 \ \ (l-k + j) / 2 \结束{数组}}\)\右]\{对齐}$ $gydF4y2Ba
(18)gydF4y2Ba
$ ${对齐}g_j& = \ \开始和_{\{数组}{c}开始k = j k = k + + 1 \ \ 2 \{数组}}结束^ \ infty左(ab) _ {kj} \[\总和_{\{数组}{c}开始l = k-j \ \ l = l + 2 \{数组}}结束^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开({\开始{数组}{c} (l - 1) / 2 \ \ (l-k + j) / 2 \结束{数组}}\)\右]\{对齐}$ $gydF4y2Ba
(19)gydF4y2Ba

和gydF4y2Ba

$ ${对齐}{}\开始(ab) _ {kj}和{:=}\压裂{1 + (1)^ j} {2} (1) ^ {j / 2} a_k + \压裂{1 + (1)^ {j - 1}}{2}(1) ^{\压裂{j - 1} {2}} b_k ={\左\{\{数组}{你}a_k开始(1)^ {j / 2}和{}\{如果}j \文本{甚至}\ \ b_k (1) ^ {(j - 1) / 2}和{}\文本{如果}j \文本{是奇数}。数组{}\ \端。}\{对齐}$ $gydF4y2Ba
(20)gydF4y2Ba

方程式的幂级数扩张。(gydF4y2Ba16gydF4y2Ba)和(gydF4y2Ba17gydF4y2Ba)的收敛半径gydF4y2Ba\ (z (t) | = | | (x (t) a_0) / A_1 | < 1 \)gydF4y2Ba70年gydF4y2Ba因此,新输入gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba必须限制gydF4y2Ba< \ \ (A_0-A_1帽子{x} (t) < A_0 + A_1 \)gydF4y2Ba。通过替换情商。gydF4y2Ba20.gydF4y2Ba)方程式。(gydF4y2Ba18gydF4y2Ba)和(gydF4y2Ba19gydF4y2Ba我们注意到每一个gydF4y2Ba\ (f_j \)gydF4y2Ba和gydF4y2Ba\ (g_j \)gydF4y2Ba系数与gydF4y2Ba\ (j \ \ mathbb {N} _0 \)gydF4y2Ba取决于傅里叶系数gydF4y2Ba\ (a_j \)gydF4y2Ba和gydF4y2Ba\ (b_j \)gydF4y2Ba通过gydF4y2Ba

$ ${对齐}f_j = &{\ \开始左\{\{数组}{你}开始f_j (a_j,现代j + 2} {\ ldots) & j文本{如果}{}\四\ \文字{甚至}\ \ f_j (b_j, b_ j + 2} {\ ldots) & j文本{如果}{}\四\ \文字{是奇数}\{数组}\右结束。}\{对齐}$ $gydF4y2Ba
(21)gydF4y2Ba
$ ${对齐}g_j = &{\ \开始左\{\{数组}{你}开始g_j(现代{j + 1},现代j + 3} {\ ldots) & j文本{如果}{}\ \文字{甚至}\ \ g_j (b_ {j + 1}, b_ j + 3} {\ ldots) & j文本{如果}{}\ \文字{是奇数}。数组{}\ \端。}\{对齐}$ $gydF4y2Ba
(22)gydF4y2Ba

请注意,gydF4y2Ba\ (f_j \)gydF4y2Ba和gydF4y2Ba\ (g_j \)gydF4y2Ba取决于不同的傅里叶系数,特别是,gydF4y2Ba\ (f_j \)gydF4y2Ba取决于甚至gydF4y2Ba\ (a_j \)gydF4y2Ba和奇怪的gydF4y2Ba\ (b_j \)gydF4y2Ba,gydF4y2Ba\ (g_j \)gydF4y2Ba取决于奇怪gydF4y2Ba\ (a_j \)gydF4y2Ba甚至gydF4y2Ba\ (b_j \)gydF4y2Ba。此外,情商的矩阵形式。gydF4y2Ba18gydF4y2Ba)是一个上三角矩阵,这意味着,如果gydF4y2Ba\ (f_j \)gydF4y2Ba系数是已知的,那么gydF4y2Ba\ (a_j \)gydF4y2Ba与gydF4y2BajgydF4y2Ba甚至和gydF4y2Ba\ (b_j \)gydF4y2Ba与gydF4y2BajgydF4y2Ba奇怪的可以计算替换回来。以模拟方式,情商。gydF4y2Ba19gydF4y2Ba)是一个上三角矩阵,这意味着,如果gydF4y2Ba\ (g_j \)gydF4y2Ba系数是已知的,那么gydF4y2Ba\ (a_j \)gydF4y2Ba与gydF4y2BajgydF4y2Ba奇怪的,gydF4y2Ba\ (b_j \)gydF4y2Ba与gydF4y2BajgydF4y2Ba甚至可以计算替换回来。为了说明这个过程,让我们假设我们计算方程式。(gydF4y2Ba18gydF4y2Ba)和(gydF4y2Ba19gydF4y2Ba),gydF4y2Ba\ (k = 4 \)gydF4y2Ba那么,这些方程的矩阵形式gydF4y2Ba

$ ${对齐}\ \开始开始{bmatrix} f_0 f \ \ \ \₂结束\ \ -f_3 \ \ f_4 \ {bmatrix} = {bmatrix} \开始1 & 0 & 1 & {}{}{}0 & {}1 \ \ 0 & 1 & 0 & {}{}{}3 & {}\ \ 0 & 0 & {}{}2 & 0 & {}{}8 \ \ 0 & 0 & 0 & {}{}{}4 & {}\ \ 0 & 0 & 0 & {}{}{}8 0 & {}\ \ \ {bmatrix}结束\ {bmatrix}开始a_0 \ \ b_1 \ \ a₂\ \ b_3 \ \ a_4 \ {bmatrix}结束\{对齐}$ $gydF4y2Ba
(23)gydF4y2Ba

和gydF4y2Ba

$ ${对齐}\ \开始开始{bmatrix} g_0 \ \ g_1里面结束\ \ -g_2 \ \ -g_3 \ {bmatrix} = {bmatrix} \开始1 & 0 & 1 & {}{}{}\ \ 0 & 2 & 0 & {}{}{}4 \ \ 0 4 & & 0 & {}{}{}\ \ 0 & 0 & 0 & {}{}{}8 \ \ \ {bmatrix}结束\ {bmatrix}开始a_1 \ \ b_2 \ \ a_3 \ \ b_4 \ {bmatrix}结束。\{对齐}$ $gydF4y2Ba
(24)gydF4y2Ba

注意,这些方程可以分为偶数和奇数的组件gydF4y2Ba

$ ${对齐}\ \开始开始{bmatrix} f_0结束\ \₂\ \ f_4 \ {bmatrix} = {bmatrix}和{}\开始1 & 1 & {}{}1 \ \ 0 & {}2 8 & {}\ \ 0 8 & 0 & {}{}\ \ \ {bmatrix}结束\ {bmatrix}开始a_0 \ \ a₂\ \ a_4 \ {bmatrix}结束\{对齐}$ $gydF4y2Ba
(25)gydF4y2Ba
$ ${对齐}\ \开始开始f {bmatrix} \ \ -f_3 \结束{bmatrix} = {bmatrix}和{}\开始1 & 3 {}\ \ 0 & {}4 \ \ \ {bmatrix} \ {bmatrix}开始结束结束b_1 \ \ b_3 \ \ \ {bmatrix} \{对齐}$ $gydF4y2Ba
(26)gydF4y2Ba
$ ${对齐}\ \开始开始{bmatrix}结束g_0 \ \ -g_2 \ \ \ {bmatrix} = {bmatrix}和{}\开始1 & {}1 \ \ 0 & 4 \ \ \ {}{bmatrix} \ {bmatrix}开始结束结束a_1 \ \ a_3 \ \ \ {bmatrix} \{对齐}$ $gydF4y2Ba
(27)gydF4y2Ba
$ ${对齐}\ \开始开始{bmatrix}结束g_1里面\ \ -g_3 \ \ \ {bmatrix} = {bmatrix}和{}\开始2 & 4 {}\ \ 0 8 & {}\ \ \ {bmatrix} \ {bmatrix}开始结束b_2 \ \ b_4 \ \ \ {bmatrix}结束。\{对齐}$ $gydF4y2Ba
(28)gydF4y2Ba

这些方程可以通过替换回去解决如上所述。同样的程序可以应用gydF4y2Ba\ (k \ \ mathbb {N} _0 \)gydF4y2Ba。方程式右边。(gydF4y2Ba16gydF4y2Ba)和(gydF4y2Ba17gydF4y2Ba)是一个多项式拟合。可视化这一事实,假设gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba是一个采样gydF4y2BaNgydF4y2Ba长度的序列,我们定义gydF4y2Ba\ (x_n = A_1 \罪(2π\ n / n) + A_0 \)gydF4y2Ba与gydF4y2Ba在[0,n - 1] \ (n \ \)gydF4y2Ba,然后gydF4y2Ba\ ((x_n-A_0) / A_1 \ [1] \)gydF4y2Ba。离散的情商。gydF4y2Ba1gydF4y2Ba)是gydF4y2Ba\(最大= f (x_n) + g (x_n) x ' _n”\)gydF4y2Ba。的傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba可以获得)gydF4y2Ba\(最大\)gydF4y2Ba通过使用FFT,这是补充M1中讨论。我们还定义gydF4y2Ba\ (z_n {: =} (x_n-A_0) / A_1 \)gydF4y2Ba,gydF4y2Ba\ (fn: = {} F (z_n) \)gydF4y2Ba和gydF4y2Ba\ (G_n {: =} G (z_n) \)gydF4y2Ba。假设我们想计算多项式扩展秩序gydF4y2Ba米gydF4y2Ba,即gydF4y2Ba\ (k_{马克斯}= M \)gydF4y2Ba,然后方程式。(gydF4y2Ba16gydF4y2Ba)和(gydF4y2Ba17gydF4y2Ba)被编写为gydF4y2Ba

$ ${对齐}fn = \ \开始和_ {j = 0} ^ {M} f_j z_n ^{对齐}$ $ j \结束gydF4y2Ba
(29)gydF4y2Ba
$ ${对齐}G_n& = \ \开始和_ {j = 0} ^ {m - 1} g_j z_n ^ j。\{对齐}$ $gydF4y2Ba
(30)gydF4y2Ba

它可以用矩阵表示形式gydF4y2Ba

$ ${对齐}\ \开始开始{bmatrix} F_0 f \ \ \ \ \ f {n} vdots \ \ \ \ \ {bmatrix} = {bmatrix} \开始结束1 & {}z_0 & {} z_0 ^ 2 & {} \ cdots & {} z_0 ^ {M} \ \ 1 & {} z_1 & {} z_1 ^ 2 & {} \ cdots & {} z_1 ^ {M} \ \ \ vdots & {} \ vdots & {} \ vdots & {} \ cdots & {} \ vdots \ \ 1 & {} z_ {n}和{}z_ {n} ^ 2 & {} \ cdots & {} z_ {n} ^ {M} \ \ \ {bmatrix}结束\ {bmatrix}开始F_0 f \ \ \ \ \ vdots f {M} \ \ \ \ \ {bmatrix}结束\{对齐}$ $gydF4y2Ba
(31)gydF4y2Ba
$ ${对齐}\ \开始开始{bmatrix} G_0 \ \ G_1里面\ \ \ vdots \ \ G_ {n} \ \ \ {bmatrix} =结束\ 1开始{bmatrix}和{}z_0和{}z_0 ^ 2 & {} \ cdots & {} z_0 ^ {m - 1} \ \ 1 & {} z_1 & {} z_1 ^ 2 & {} \ cdots & {} z_1 ^ {m - 1} \ \ \ vdots & {} \ vdots & {} \ vdots & {} \ cdots & {} \ vdots \ \ 1 & {} z_ {n}和{}z_ {n} ^ 2 & {} \ cdots & {} z_ {n} ^ {m - 1} \ \ \ {bmatrix}结束\ {bmatrix}开始G_0 \ \ G_1里面\ \ \ vdots \ \ G_ {m - 1} \ \ \ {bmatrix}结束。\{对齐}$ $gydF4y2Ba
(32)gydF4y2Ba

右边的矩阵称为范德蒙矩阵。如果gydF4y2Ba\ (fn \)gydF4y2Ba和gydF4y2Ba\ (G_n \)gydF4y2Ba多项式的系数是已知的,那么得到的反演范德蒙矩阵。如果所有的gydF4y2Ba\ (z_n \)gydF4y2Ba条件是不同的,然后方程式。(gydF4y2Ba29日gydF4y2Ba)和(gydF4y2Ba30.gydF4y2Ba)是可逆的,当gydF4y2Ba\ ((M + 1) \ N \)gydF4y2Ba和gydF4y2Ba\ (M \ N \)gydF4y2Ba,分别。这限制了多项式的最大订单gydF4y2Ba\ (M_{马克斯}= n - 1 \)gydF4y2Ba。通过定义范德蒙矩阵方程式。(gydF4y2Ba31日gydF4y2Ba)和(gydF4y2Ba32gydF4y2Ba),gydF4y2Ba\ ({\ textbf {Z}} _ {M} \)gydF4y2Ba和gydF4y2Ba\ ({\ textbf {Z}} _ {m - 1} \)gydF4y2Ba,我们可以写gydF4y2Ba

$ ${对齐}\ \开始开始vec {F} ={对齐}\ & {\ textbf {Z}} _ {M} \ cdot \ vec vec {G} {F} \ \ \ = & {\ textbf {Z}} _ {M - 1} \ cdot vec {G} \ \{对齐}结束\{对齐}$ $gydF4y2Ba
(33)gydF4y2Ba

和解决方案的最小二乘法估计gydF4y2Ba

$ ${对齐}\ \开始离开({\ textbf {Z}} _ {M} ^ T \ cdot {\ textbf {Z}} _ {M} \右)^ {1}\ cdot {\ textbf {Z}} _ {M} ^ T \ cdot \ vec vec {F} {F} = & \ \{对齐}$ $gydF4y2Ba
(34)gydF4y2Ba
$ ${对齐}\ \开始离开({\ textbf {Z}} _ {m - 1} ^ T \ cdot {\ textbf {Z}} _ {m - 1} \右)^ {1}\ cdot {\ textbf {Z}} _ {m - 1} ^ T vec {G} = & \ \ cdot \ vec {G}。\{对齐}$ $gydF4y2Ba
(35)gydF4y2Ba

方程(gydF4y2Ba34gydF4y2Ba)和(gydF4y2Ba35gydF4y2Ba)对应于两个多项式回归的问题。最后,我们得出结论,方程式。(gydF4y2Ba16gydF4y2Ba)和(gydF4y2Ba17gydF4y2Ba)显示一个傅里叶分析和两个多项式配件之间的等价性。事实上,FFT算法利用一个类似的等价之间的复杂的傅里叶级数和多项式扩张,看到裁判。gydF4y2Ba71年gydF4y2Ba和引用。参见补充M2,我们讨论这项工作通过假设的形式动态变量gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)作为一个复杂的功能。gydF4y2Ba

然而,该协会的gydF4y2Ba\ (f_j \)gydF4y2Ba和gydF4y2Ba\ (g_j \)gydF4y2Ba系数,系数多项式回归的特性曲线gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2Ba\ \ (x (A_0-A_1, A_0 + A_1) \)gydF4y2Ba定义在情商。gydF4y2Ba1gydF4y2Ba)的傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)不是报告文学。方程(gydF4y2Ba12gydF4y2Ba),(gydF4y2Ba16gydF4y2Ba)和(gydF4y2Ba17gydF4y2Ba)表明,傅里叶分析gydF4y2Ba\ (y (t) = f (x (t)) + g (x (t)) x (t) \)gydF4y2Ba与gydF4y2Ba罪\ (x (t) = A_1 \{\ωt} + A_0 \)gydF4y2Ba相当于的多项式回归gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2Ba\ \ (x (A_0-A_1, A_0 + A_1) \)gydF4y2Ba此外,gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba取决于不同的傅里叶系数,因此,他们是独立的。在电路理论的语言,注意到gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba)与一个电阻和电抗元件的特性曲线,分别论证在最后一句话意味着在给定的一阶系统,如果电抗元件是由另一个改变,相对应的傅里叶系数电阻元件必须保持不变。同样,如果电阻元件是由另一个改变,相对应的傅里叶系数电抗元件必须保持不变。gydF4y2Ba

实现gydF4y2Ba

基于实验或仿真数据的实现方法,我们使用连续时间变量主要作为离散采样版本的动态变量,只在特定时间已知的驱动力。为了简单起见,我们考虑一个统一时间变量已知每个抽样方案gydF4y2Ba\ (T_s \)gydF4y2Ba秒,gydF4y2Ba\ (T_s \)gydF4y2Ba是采样周期。这让我们获得的傅里叶级数系数的FFT算法,补充M1的解释。gydF4y2Ba

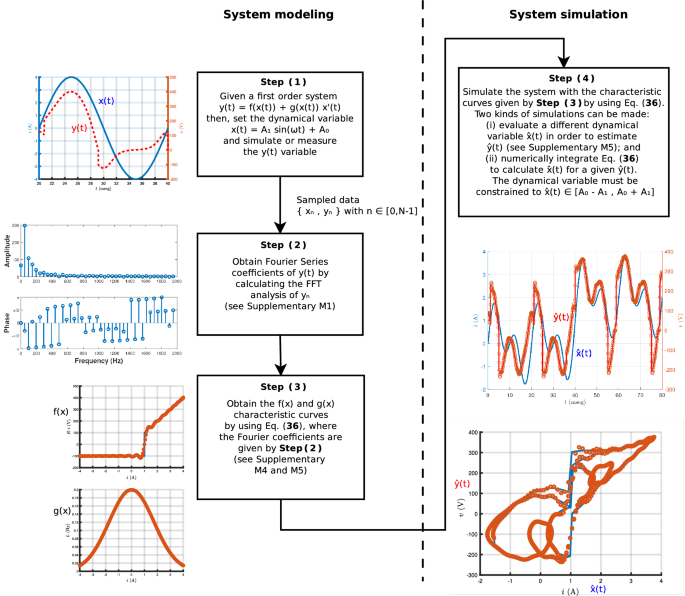
建模和模拟的过程基于这样的工作反映在图的形式主义。gydF4y2Ba1gydF4y2Ba。它由四个步骤的盒子图。方法可分为两个主要部分:第一个是特性曲线的估计基于FFT的采样数据gydF4y2Ba\ \ {x_n,推出\}\)gydF4y2Ba与gydF4y2Ba\ (n = [0, n - 1] \)gydF4y2Ba和Eq的使用。gydF4y2Ba36gydF4y2Ba),这相当于情商。gydF4y2Ba12gydF4y2Ba),但计算速度;第二个是时域仿真用情商。gydF4y2Ba36gydF4y2Ba)。在接下来的段落我们讨论如何获得更快的计算方程,并进一步分析了补充M3。情商的MATLAB代码实现。gydF4y2Ba36gydF4y2Ba)提出了补充M4。盒子周围的图像在无花果gydF4y2Ba1gydF4y2Ba显示每一步的预期输出,改编自一个例子中提供补充M5。gydF4y2Ba

图1gydF4y2Ba
图1gydF4y2Ba

原理图对系统建模和仿真的方法基于这项工作的形式主义。盒子周围的插图显示每一步的预期输出,改编自一个例子中提供补充M5。方法由连续应该应用的四个主要步骤:(1)确定一阶方程和动力学变量设置为一个语气谐波输入;(2)计算响应的傅里叶级数系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba),获得振幅和相位傅里叶分析;(3)获得的特性曲线评价情商。gydF4y2Ba36gydF4y2Ba);(4)使用相同的系统仿真特性曲线,两个选项:(i)计算gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba对于任意一个动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba,不一定是一个基调;和(2)计算gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba对于一个给定的gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba。在这两种情况下的约束gydF4y2Ba\(\帽子{x} (t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba必须满足。gydF4y2Ba

全尺寸图像gydF4y2Ba

在剩下的部分,我们将讨论如何情商。gydF4y2Ba36gydF4y2Ba)是计算优惠,然后,我们存在一些技术方面的细节为每个步骤的实现。在gydF4y2Ba形式主义gydF4y2Ba节中,我们用gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba在情商。gydF4y2Ba10gydF4y2Ba)获得情商。gydF4y2Ba12gydF4y2Ba),这有助于我们想象的傅里叶级数和幂级数之间的联系,但是对于计算提出了有利的进行替换为情商。(gydF4y2Ba9gydF4y2Ba)。然后,以下表达式gydF4y2Ba

$ ${对齐}\ \开始开始{对齐}y (t) & = \ underbrace左{\ [a_0 + \总和_ {k = 1} ^ \ infty \总和_{\{数组}}{c l = 0开始结束\ \ l = l + 2 \{数组}}^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开(1 - \离开(\压裂{x (t) a_0} {A_1} \右)^ 2 \右)^ {l / 2} \离开(\压裂{x (t) a_0} {A_1} \右)^ {k-l} (ab) _ {kl} \]} _ {= f (x (t))} \ \ &左\四+ \ underbrace{\[\总和_ {k = 1} ^ \ infty \总和_{\{数组}{c}开始l = 1 \ \ l = l + 2 \{数组}}结束^ k \离开({\{数组}{c}开始结束k l \ \ \{数组}}\)\离开(1 - \离开(\压裂{x (t) a_0} {A_1} \右)^ 2 \右)^ {(l - 1) / 2} \离开(\压裂{x (t) a_0} {A_1} \右)^ {k-l} (ab) _ {kl} \] \压裂{1}{一个“_1}}_ {= g (x (t))} \, x (t) \{对齐}结束\{对齐}$ $gydF4y2Ba
(36)gydF4y2Ba

在哪里gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba特性曲线已确定。方程(gydF4y2Ba36gydF4y2Ba)双求和代替Eq。(gydF4y2Ba12gydF4y2Ba)三合计,这意味着他们有一个计算的复杂性gydF4y2Ba\ (\ mathscr {O} (N k_{马克斯}^ 2)\)gydF4y2Ba和gydF4y2Ba\ (\ mathscr {O} (N k_{马克斯}^ 3)\)gydF4y2Ba,分别。详细分析了补充M3。这意味着情商。gydF4y2Ba36gydF4y2Ba)是计算的,它的使用是首选的实际实现。gydF4y2Ba

并给出了实现的一些技术细节。我们考虑到动态变量gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)和驱动力gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)是由采样序列gydF4y2Ba\ (x_n \)gydF4y2Ba和gydF4y2Ba\(最大\)gydF4y2Ba,gydF4y2Ba\ (n = [0, n - 1] \)gydF4y2Ba。这种考虑是基于事实,在模拟或从一个实验数据采集,连续变量的时间演化主要是由这些变量的采样版本。连续时间变量可以从抽样数据的重建考虑Nyquist-Shannon-Whitaker抽样定理gydF4y2Ba72年gydF4y2Ba,gydF4y2Ba73年gydF4y2Ba。采样数据使我们能够计算傅里叶系数gydF4y2Ba\ (a_k \)gydF4y2Ba和gydF4y2Ba\ (b_k \)gydF4y2Ba从FFT分析,使我们能够利用FFT算法计算快gydF4y2Ba74年gydF4y2Ba。短暂的傅里叶级数和FFT分析之间的关系给出了补充M1。gydF4y2Ba

曾经的傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)是经FFT分析,我们可以利用情商。gydF4y2Ba36gydF4y2Ba)获得gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba特性曲线。这些特性曲线定义的系统,这意味着他们不改变即使我们考虑其他动态变量或驱动力。这个事实可以被利用来模拟其他动态变量和驱动力,利用这些特性曲线。接下来,我们将讨论一些技术细节的实现的每一步gydF4y2Ba

步骤(1)::gydF4y2Ba

设置一个正弦动态变量gydF4y2Ba\ \ (x (t) ! = \ !一个_1\sin (\omega t)+A_0\)进入系统,以模拟或测量gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)反应。一个说明性的例子显示在左边的图中相应的盒子。gydF4y2Ba1gydF4y2Ba。的gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)信号通常是由采样序列gydF4y2Ba\ \ {x_n,推出\}\)gydF4y2Ba与gydF4y2Ba在[0,n - 1] \ (n \ \)gydF4y2Ba。这个信号采样表示的值定义为测量每一个连续函数gydF4y2Ba\ (T_s \)gydF4y2Ba秒,gydF4y2Ba\ (T_s \)gydF4y2Ba是采样周期。考虑一个周期gydF4y2Baω\ (T = 2 \π/ \ \)gydF4y2Ba的正弦动态变量,然后取样长度gydF4y2BaNgydF4y2Ba被定义为gydF4y2Ba\ (N = T / T_s \)gydF4y2Ba,即它所代表的数量在一个周期内的采样序列。gydF4y2Ba

步骤(2)::gydF4y2Ba

傅里叶系数的计算gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)的FFT向量gydF4y2Ba\ (vec {y} = \ [\ ldots y_0, y_1, y_ {n}] \)gydF4y2Ba,由采样序列gydF4y2Ba\(最大\)gydF4y2Ba连续变量的gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)。FFT快速算法gydF4y2Ba74年gydF4y2Ba计算离散傅里叶变换(DFT)计算复杂度gydF4y2Ba\ (\ mathscr {O} (N \ ln {N}) \)gydF4y2Ba。DFT的结果是agydF4y2BaNgydF4y2Ba长度复杂的矢量,这通常是由双面振幅和相位傅里叶频谱。等真正的序列,测量的是一个真正的大小gydF4y2Ba\(最大\)gydF4y2Ba,通常使用单面振幅和相位傅里叶谱的表示,因为它是显示在左边的一步gydF4y2Ba(2)gydF4y2Ba在无花果。gydF4y2Ba1gydF4y2Ba。补充M1显示之间的对应关系的单面傅里叶谱和傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)。gydF4y2Ba

步骤(3)::gydF4y2Ba

评估特性曲线gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba)通过使用Eq。(gydF4y2Ba36gydF4y2Ba),参数的值gydF4y2Ba\ (A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba,gydF4y2Ba\ (A_1 ' =ωA_1 \ \)gydF4y2Ba的傅里叶系数gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)得到的正弦动态变量。情商的实际实现。gydF4y2Ba36gydF4y2Ba)需要一些gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba外求和的值,这个值是谐波的最大数量,将被认为是在分析。见补充M1,理论最大值gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba是gydF4y2Ba\ (k_{马克斯}= \ lfloor \压裂{N} {2} \ rfloor - \压裂{1 + (1)^ N} {2} \)gydF4y2Ba。然而,分析补充M6,一些数字舍入错误可能会出现gydF4y2Ba\ (k_{马克斯}> 50 \)gydF4y2Ba。的更大的价值gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba避免这些舍入错误发现gydF4y2Ba\ (k_{马克斯}= 40 \)gydF4y2Ba。然而,值得提醒的是,通过使用其他数值技术评估方面的总和,它甚至可能考虑在必要时更高的谐波量。通过评估gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba根据情商)特性曲线。gydF4y2Ba36gydF4y2Ba),我们能够获得系统建模,左边所示的步骤gydF4y2Ba(3)gydF4y2Ba在无花果。gydF4y2Ba1gydF4y2Ba。gydF4y2Ba

步骤(4)::gydF4y2Ba

用情商。gydF4y2Ba36gydF4y2Ba)时域仿真。提出了两种模拟:(i)第一个由评估Eq。(gydF4y2Ba36gydF4y2Ba)新已知动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba为了估计相应的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba;(2)和第二个由使用一个已知的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba为了获得gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba基于数值积分的情商。gydF4y2Ba36gydF4y2Ba)。在这两种情况下的约束gydF4y2Ba\(\帽子{x} (t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba必须满足。重要的是要强调gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba和gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba被修改,但必须保持固定模型参数值获得正弦响应的步骤吗gydF4y2Ba(2)gydF4y2Ba。为了说明模拟的种类(1),我们提出两个插图下面图中相应的盒子。gydF4y2Ba1gydF4y2Ba:第一个显示给定动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba及其相应的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba实线,驱动力的计算基于情商。gydF4y2Ba36gydF4y2Ba)圆圈所示;和第二个节目gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba对gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba,其中实线理论模拟的结果和圆圈对应的预测值gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba通过使用情商。gydF4y2Ba36gydF4y2Ba)。这说明性的例子的细节,一步一步的实现方法提出了补充M5。出于完整性的考虑,我们提出一些注意事项(2)以下。基本思想是使用特性曲线(完全定义的系统),计算动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba基于一个已知的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba。通过求解情商。gydF4y2Ba36gydF4y2Ba)gydF4y2Ba\(\帽子{x}’(t) \)gydF4y2Ba,我们获得gydF4y2Ba

$ ${对齐}\ \开始帽子{x} ' (t) = \压裂{{y} \帽子(t) - f(\帽子{x} (t)} {g(\帽子{x} (t)}。\{对齐}$ $gydF4y2Ba
(37)gydF4y2Ba

方程(gydF4y2Ba37gydF4y2Ba)可以通过使用数字集成,例如,欧拉方法gydF4y2Ba75年gydF4y2Ba

$ $ \开始{对齐}{\左\{{数组}{你}\ \开始帽子{x} (t_0) = x_0 \ \ {x} (t_n) = \ \帽子帽子{x} (t_ {n}识别)+ (t_n-t_ {n}) \;\ dfrac {{y} \帽子(t_ {n})识别- f(\帽子{x} (t_ {n})识别)}{g(\帽子{x} (t_ {n})识别)}\四n \通用电气1 \结束数组{}\。}\{对齐}$ $gydF4y2Ba
(38)gydF4y2Ba

在哪里gydF4y2Ba\ (x_0 \)gydF4y2Ba初始条件和吗gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba定义在情商。gydF4y2Ba36gydF4y2Ba)。方程(gydF4y2Ba38gydF4y2Ba)让我们来计算动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba从已知的驱动力gydF4y2Ba\ ({y} (t) \ \帽子)gydF4y2Ba。如果时间步gydF4y2Ba\ (t_n-t_ {n} \)gydF4y2Ba不是足够小,情商的使用。(gydF4y2Ba38gydF4y2Ba)可能屈服于数值错误。在这些情况下,可以使用更复杂的集成方法,比如修的方法gydF4y2Ba75年gydF4y2Ba

$ $ \开始{对齐}{\左\{{数组}{你}\ \开始帽子{x} (t_0) = x_0 \ \ \波浪号{x} (t_n) = {x} \帽子(t_ {n}识别)+ (t_n-t_ {n}) \;\ dfrac {{y} \帽子(t_ {n})识别- f(\帽子{x} (t_ {n})识别)}{g(\帽子{x} (t_ {n})识别)}\ \ {x} (t_n) = \ \帽子帽子{x} (t_ {n})识别+ \ dfrac {t_n-t_ {n}} {2} \;左(\ \ dfrac {{y} \帽子(t_ {n})识别- f(\帽子{x} (t_ {n})识别)}{g(\帽子{x} (t_ {n})识别)}+ \ dfrac {{y} \帽子(t_ {n})识别- f(\波浪号{x} (t_ {n})识别)}{g(\波浪号{x} (t_ {n})识别)}\)\四n \通用电气1 \{数组}\右结束。}\{对齐}$ $gydF4y2Ba
(39)gydF4y2Ba

修的两种评估方法需要情商。gydF4y2Ba36gydF4y2Ba每个集成步骤),因此,计算时间的两倍。在补充M5中给出的例子中,我们使用方程式得到几乎相同的结果。(gydF4y2Ba38gydF4y2Ba)和(gydF4y2Ba39gydF4y2Ba),因此,只有情商的结果。gydF4y2Ba38gydF4y2Ba)。gydF4y2Ba

应用程序gydF4y2Ba

这个工作的方法可以应用于任何动态方程,可以扔在情商的一阶系统。gydF4y2Ba1gydF4y2Ba)。注意左边的情商。gydF4y2Ba1gydF4y2Ba)是一个依赖于时间的可测量的数量和右边只取决于动态变量及其一阶导数。更显式表达式情商研究动态。gydF4y2Ba1gydF4y2Ba)是由gydF4y2Ba

$ $ \{对齐}开始x (t) = (y (t) - F (x (t))) / g (x (t)) {: =} F (x (t) y (t)), \{对齐}$ $gydF4y2Ba
(40)gydF4y2Ba

的函数gydF4y2BaFgydF4y2Ba显示的依赖gydF4y2Ba\ (x (t) \)gydF4y2Ba与gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)。这个方程可以用不同的方式注意情商。gydF4y2Ba2gydF4y2Ba),gydF4y2BatgydF4y2Ba是与gydF4y2Baω\ (\ \)gydF4y2Ba因此我们可以定义一个函数gydF4y2BaY(\ \(ω(t)) {: =} Y (t) \)gydF4y2Ba,在那里gydF4y2Ba\ \(ω(t){: =} \ωt \)gydF4y2Ba,然后gydF4y2Ba

$ $ \开始{对齐}{\左\{\{数组}{你}开始x”(t) = F (x (t), Y(\ω(t))) \ \ \ω”(t) =ω\ \{数组}\右结束。}\{对齐}$ $gydF4y2Ba
(41)gydF4y2Ba

我们基本上改变了情商的一阶系统。gydF4y2Ba1gydF4y2Ba)一个自治的二阶系统。在本节中,我们首先讨论一些简单的系统,一般情况下非线性RL系列和并行RC系统。这两个系统是用于补充M5呈现四个示范例子:一个非连续的非线性电感串联电阻、二极管,二极管并联电容器,和一个非线性电感器。然后,在本节中,我们提出一个方法应用形式主义RL和RC系统,我们写系统方程为一个方便的形式基于一分之二阶方程。gydF4y2Ba

著名的电器元件之间的类比gydF4y2BaRgydF4y2Ba,gydF4y2BalgydF4y2Ba和gydF4y2BaCgydF4y2Ba和机械类gydF4y2BabgydF4y2Ba,gydF4y2Ba米gydF4y2Ba和gydF4y2BakgydF4y2Ba34gydF4y2Ba,并与其他领域如音响、热量和水力学,允许我们应用作为一个多学科的方法工具。更多的细节详细研究了类比,例如,通过键合图理论gydF4y2Ba76年gydF4y2Ba,gydF4y2Ba77年gydF4y2Ba。gydF4y2Ba

有许多特定的潜在应用,可以探索使用这种形式,在剩下的部分,我们现在只有几个领域:电子测量,在一个假想的装置称为“非线性电感电容电阻测量计”了;粘弹性材料;机械和结构动力学,我们讨论一个简单的例子估计非线性机械系统的阻尼作用。gydF4y2Ba

这还需要进一步的研究来阐明如果形式能够完全代表磁滞和非线性共振等一些重要的现象。在“gydF4y2Ba讨论gydF4y2Ba”部分,我们提出一个更详细的分析的局限性和进一步研究方向,以阐明的范围和范围的应用形式。gydF4y2Ba

非线性RL系列系统gydF4y2Ba

图2gydF4y2Ba
图2gydF4y2Ba

RL串联电路。gydF4y2Ba

全尺寸图像gydF4y2Ba

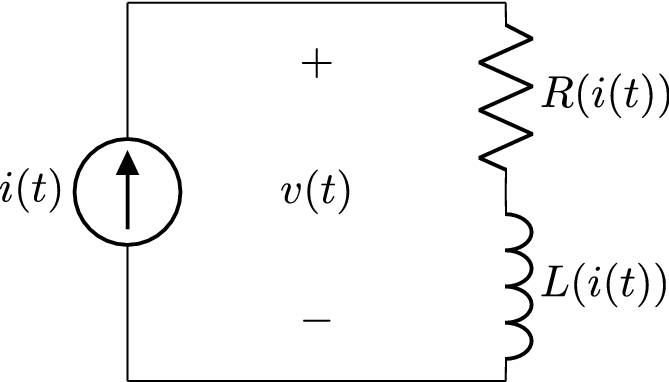
我们考虑图的电路。gydF4y2Ba2gydF4y2Ba。一方面,如果组件是基于线性关系,电压gydF4y2BavgydF4y2Ba是由电阻和电感贡献的总和gydF4y2Ba

$ $ \{对齐}开始v (t) = R \;我(t) + L \;我的(t) \{对齐}$ $gydF4y2Ba
(42)gydF4y2Ba

电阻器的本构关系在哪里gydF4y2Ba= R \ \ (v_R (t); i_R (t) \)gydF4y2Ba和电感gydF4y2BaL = \ \ (v_L (t); i_L”(t) \)gydF4y2Ba被使用。另一方面,如果组件是非线性,电阻和电感可以被认为是当前的依赖,因此情商。gydF4y2Ba42gydF4y2Ba)改变成gydF4y2Ba

$ $ \{对齐}开始v (t) = R(我(t)) \我(t) + L(我(t)) \我(t)。\{对齐}$ $gydF4y2Ba
(43)gydF4y2Ba

注意,非线性电阻代表任何组件可以定义为一个电流-电压特性曲线,如二极管或晶体管。方程(gydF4y2Ba43gydF4y2Ba)提出了相同的函数依赖的情商。gydF4y2Ba36gydF4y2Ba)。如果设置动态变量gydF4y2Ba\(我(t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba的傅里叶级数gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba)将与情商。gydF4y2Ba36gydF4y2Ba),gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)所取代gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)所取代gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba)。特性曲线可以确定为gydF4y2Ba

$ $ \{对齐}开始f(我(t); \ {a_k, b_k \}, A_0, A_1) = R(我(t)) \;我(t) \{对齐}$ $gydF4y2Ba
(44)gydF4y2Ba

和gydF4y2Ba

$ $ \{对齐}g(开始我(t); \ {a_k, b_k \}, A_0, A_1, A_1 ') = L(我(t)), \{对齐}$ $gydF4y2Ba
(45)gydF4y2Ba

在哪里gydF4y2Ba\ \ {a_k, b_k \} \)gydF4y2Ba的傅里叶系数吗gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba)gydF4y2Ba\(我(t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 ' = \马克斯(我(t)) =ωA_1 \ \)gydF4y2Ba。总之,基于响应的傅里叶分析gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba从一个正弦动态变量gydF4y2Ba\(我(t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,我们得到一个精确的计算表达式gydF4y2BaRgydF4y2Ba(gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba)),gydF4y2BalgydF4y2Ba(gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba))。方程(gydF4y2Ba43gydF4y2Ba)必须保持相同的功能依赖与其他动态变量gydF4y2Ba\ \(帽子{我}(t) \)gydF4y2Ba因此,相应的驱动力gydF4y2Ba\(\帽子}{v (t) \)gydF4y2Ba必须验证gydF4y2Ba

$ ${对齐}\ \开始帽子}{v (t) = R(\帽子{我}(t); \ {a_k, b_k \}, A_0, A_1) \ \帽子{我}(t) + L(\帽子{我}(t); \ {a_k, b_k \}, A_0, A_1, A_1) \ \帽子{我}’(t) \{对齐}$ $gydF4y2Ba
(46)gydF4y2Ba

提供动态变量限制范围gydF4y2Ba\(\帽子{我}(t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。gydF4y2Ba

非线性并行RC系统gydF4y2Ba

图3gydF4y2Ba
图3gydF4y2Ba

RC并联电路。gydF4y2Ba

全尺寸图像gydF4y2Ba

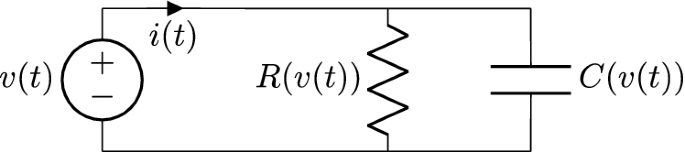
考虑图的电路。gydF4y2Ba3gydF4y2Ba)。本构方程的非线性电阻器和电容器可以被认为是电压的依赖,gydF4y2Ba\ (v_R (t) = R (v_R (t)) \; i_R (t) \)gydF4y2Ba和gydF4y2Ba\ (q (t) = C (v_c (t)) \; v_c (t) \)gydF4y2Ba,分别。然后,功能动态变量之间的依赖gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba)和当前gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba)可以写成gydF4y2Ba

$ $ \{对齐}我开始(t) & = i_R (t) + i_C (t) \ nonumber \ \ & = \ underbrace{\压裂{1}{R (v (t))}} _ {{: =} P (v (t))} v (t) + \ underbrace{\离开(\压裂{d C (v (t))}} {d v (t) + C (v (t))) \右)}_ {{:=}Q (v (t))}”v (t) \{对齐}$ $gydF4y2Ba
(47)gydF4y2Ba

用链式法则在第二项,和P和Q函数定义备查。如果设置动态变量gydF4y2Ba\ (v (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba的傅里叶级数gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba)将与情商。gydF4y2Ba36gydF4y2Ba),gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)所取代gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba)所取代gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba)。在这个例子中,当前对应的驱动力和电压动态变量的符号。特性曲线可以确定为gydF4y2Ba

$ $ \{对齐}开始f (v (t); \ {a_k, b_k \}, A_0, A_1) = P (v (t)) \ v (t) \{对齐}$ $gydF4y2Ba
(48)gydF4y2Ba

和gydF4y2Ba

$ $ \{对齐}开始g (v (t); \ {a_k, b_k \}, A_0, A_1, A_1 ') = Q (v (t)) \{对齐}$ $gydF4y2Ba
(49)gydF4y2Ba

在哪里gydF4y2Ba\ \ {a_k, b_k \} \)gydF4y2Ba的傅里叶系数吗gydF4y2Ba我gydF4y2Ba(gydF4y2BatgydF4y2Ba)gydF4y2Ba\ (v (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,gydF4y2Ba\(“_1 = \马克斯(v (t)) =ωA_1 \ \)gydF4y2Ba。方程(gydF4y2Ba47gydF4y2Ba)必须保持相同的功能依赖与其他动态变量gydF4y2Ba\(\帽子}{v (t) \)gydF4y2Ba因此,相应的驱动力gydF4y2Ba\ \(帽子{我}(t) \)gydF4y2Ba必须验证gydF4y2Ba

$ ${对齐}\ \开始帽子{我}(t) = P(\帽子}{v (t); \ {a_k, b_k \}, A_0, A_1) \ \帽子}{v (t) + Q(\帽子}{v (t); \ {a_k, b_k \},,, A_0 A_1, A_1) \ \帽子{v}’(t) \{对齐}$ $gydF4y2Ba
(50)gydF4y2Ba

提供动态变量限制范围gydF4y2Ba\(\帽子}{v (t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。gydF4y2Ba

RL和RC的组合系统gydF4y2Ba

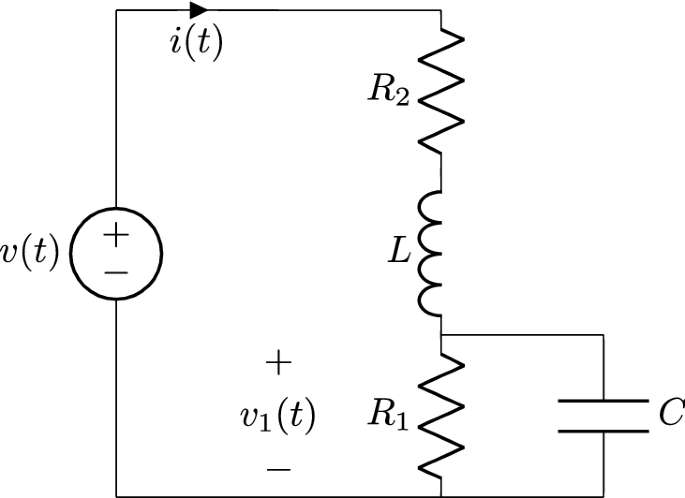
图4gydF4y2Ba
图4gydF4y2Ba

RL系列和RC并联电路。gydF4y2Ba

全尺寸图像gydF4y2Ba

RL和RC系统图所示。gydF4y2Ba4gydF4y2Ba。这个系统有两个活性成分L和C,因此有两个动态变量gydF4y2Ba\(我(t) = i_L (t) \)gydF4y2Ba和gydF4y2Ba\ (v_1 (t) = v_C (t) \)gydF4y2Ba。如果所有的组件都是非线性,系统方程可以写成一分之二阶非线性系统gydF4y2Ba

$ $ \{对齐}开始v (t) v_1 (t) = & {} R_2(我(t)) \;我(t) + L(我(t)) \;我(t) \{对齐}$ $gydF4y2Ba
(51)gydF4y2Ba
$ $ \{对齐}我开始(t) = &{} \压裂{1}{R_1 (v_1 (t))} v_1 (t) + \离开(\压裂直流(v_1 (t)) {} {dv_1} v_1 (t) + C (v_1 (t)) \右)v_1”(t) \{对齐}$ $gydF4y2Ba
(52)gydF4y2Ba

为了使用的形式为二阶系统工作,有必要单独模型每个动态变量。这意味着子系统组成的gydF4y2Ba\ (R_2 \)gydF4y2Ba和gydF4y2BalgydF4y2Ba必须研究部分中解释的方法吗gydF4y2Ba非线性RL系列系统gydF4y2Ba,组成的一个gydF4y2Ba\ (R_1 \)gydF4y2Ba和gydF4y2BaCgydF4y2Ba必须研究方法解释”gydF4y2Ba非线性并行RC系统gydF4y2Ba”。gydF4y2Ba

通过建模每个活性元素L和C作为非线性RL和并行RC系列系统,这些因素可以扩展到高阶系统。一个潜在的方法来分析在未来的工作,这可能被视为一种泛化的线性电路理论非线性电路理论,分析高阶系统。系统建模可以得到每个动态变量设置为一个基调,通过计算FFT相应的驱动力。总之,我们应该使用gydF4y2Ba非线性RL系列系统gydF4y2Ba为每一个电感器和方法gydF4y2Ba非线性并行RC系统gydF4y2Ba系统中每个电容器。gydF4y2Ba

非线性电感电容电阻测量计gydF4y2Ba

LCR测量仪主要是一种设备,适用于正弦单音的样本和措施响应的振幅和相位为了获得一系列的线性参数RL或平行的RC模型系统在给定固定的频率。作为一个直接后果的部分”gydF4y2Ba非线性RL系列系统gydF4y2Ba”和“gydF4y2Ba非线性并行RC系统gydF4y2Ba”,设计一个假设的可能性似乎“非线性电感电容电阻测量计”。提到一个众所周知的事实是很重要的在材料科学,大多数电动组件和材料是频率依赖性,这意味着特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba必须依赖于频率,即。gydF4y2Baf (x (t); \ \(ω)\)gydF4y2Ba和gydF4y2Ba\ (g (x (t); \ω)\)gydF4y2Ba。此外,还有一个设备称为“阻抗分析仪”,这给我们的线性组件平行RC或RL系列模型在给定的频率范围。这个工作的形式不包括这些频率的依赖关系。然而许多材料常量值的RL系列或平行RC组件在一个广泛的频率,是这样,例如,铁氧体电感的RL系列组件从一个阻抗分析仪获得大约持续低于MHz范围。这些材料,非线性模型的基础上,形式化的工作预计正确描述系统参数frequency-independent范围。进一步考虑应该仔细考虑解决这个频率依赖的系统,其中有一些是在“gydF4y2Ba讨论gydF4y2Ba”一节。gydF4y2Ba

粘弹性材料gydF4y2Ba

粘弹性材料的粘性和弹性性质。粘弹性的研究是重要的聚合物科学、生物力学和生物学gydF4y2Ba78年gydF4y2Ba。在这里,我们现在使用的两个简单的模型的形式主义,麦克斯韦和开耳文模型。麦克斯韦模型被定义为gydF4y2Ba

$ ${对齐}\ \开始压裂{d \ varepsilon (t)} {dt} = \压裂{1}{\埃塔}\;\σ(t) + \压裂{1}{E} \;\压裂{d \σ(t)} {dt}, \{对齐}$ $gydF4y2Ba
(53)gydF4y2Ba

在哪里gydF4y2Baσ\ (\ \)gydF4y2Ba是压力,gydF4y2Ba\ \ varepsilon \ ()gydF4y2Ba应变,gydF4y2BaEgydF4y2Ba刚度和gydF4y2Ba\埃塔(\ \)gydF4y2Ba材料的粘度。情商的非线性等效表达式。gydF4y2Ba53gydF4y2Ba)是由gydF4y2Ba

$ ${对齐}\ \开始压裂{d \ varepsilon (t)} {dt} = \压裂{1}{\埃塔(\σ(t))} \;\σ(t) + \压裂{1}{E(\σ(t))} \;\压裂{d \σ(t)} {dt}, \{对齐}$ $gydF4y2Ba
(54)gydF4y2Ba

所谓的材料常数,gydF4y2Ba\埃塔(\ \)gydF4y2Ba和gydF4y2BaEgydF4y2Ba是依赖于gydF4y2Baσ\ (\ \)gydF4y2Ba。通过比较情商。gydF4y2Ba54gydF4y2Ba)与情商。gydF4y2Ba1gydF4y2Ba),我们确定的驱动力gydF4y2Ba\ (y (t) = d \ varepsilon (t) / dt \)gydF4y2Ba,动态变量gydF4y2Ba\ (x (t) =σ(t) \ \)gydF4y2Ba和特性曲线gydF4y2Ba\ (f (x (t)) = 1 / \ησ(t)(\) \σ(t) \)gydF4y2Ba和gydF4y2Ba\ (g (x (t)) = 1 / E(\σ(t)) \)gydF4y2Ba。这意味着,根据情商。gydF4y2Ba36gydF4y2Ba),系统建模是通过傅里叶分析的计算获得gydF4y2Ba\ (d \ varepsilon (t) / dt \)gydF4y2Ba当动态变量是一个单音,即。gydF4y2Ba\ \(σ(t) =罪\{\ωt} + A_0 \)gydF4y2Ba。然后,我们可以计算特性曲线和使用系统仿真。根据图。gydF4y2Ba1gydF4y2Ba可以做两种模拟:(1)计算的驱动力gydF4y2Ba{\ \ (d \帽子varepsilon} (t) / dt \)gydF4y2Ba对应于任意动态变量gydF4y2Ba{\ \(\帽子σ}(t) \)gydF4y2Ba;和(2)计算动态变量基于一个已知的驱动力。在这两种情况下,我们必须考虑到限制gydF4y2Ba{\ \(\帽子σ}(t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。gydF4y2Ba

开耳文模型被定义为gydF4y2Ba

$ ${对齐}\ \开始σ(t) = E \ \ varepsilon (t) + \埃塔\;\ \压裂{d varepsilon (t)} {dt},{对齐}$ $ \结束gydF4y2Ba
(55)gydF4y2Ba

和它是由非线性表达式gydF4y2Ba

$ ${对齐}\ \开始σ(t) = E (\ varepsilon (t)) \ \ varepsilon (t) + \埃塔(\ varepsilon (t)) \;\ \压裂{d varepsilon (t)} {dt},{对齐}$ $ \结束gydF4y2Ba
(56)gydF4y2Ba

在哪里gydF4y2BaEgydF4y2Ba和gydF4y2Ba\埃塔(\ \)gydF4y2Ba取决于应变gydF4y2Ba\ \ varepsilon \ ()gydF4y2Ba。通过比较情商。gydF4y2Ba56gydF4y2Ba)与情商。gydF4y2Ba1gydF4y2Ba),我们确定的驱动力gydF4y2Ba\ (y (t) = \σ(t) \)gydF4y2Ba,动态变量gydF4y2Ba\ (x (t) = \ varepsilon (t) \)gydF4y2Ba和特性曲线gydF4y2Ba\ (f (x (t)) = E (\ varepsilon (t)) \;\ \ varepsilon (t))gydF4y2Ba和gydF4y2Ba\ (g (x (t)) = \埃塔(\ varepsilon (t)) \)gydF4y2Ba。系统建模是通过傅里叶分析的计算gydF4y2Ba\σ(t) (\ \)gydF4y2Ba当动态变量是一个单音,即。gydF4y2Ba\ (\ varepsilon (t) =罪\{\ωt} + A_0 \)gydF4y2Ba。然后,该模型可用于两种类型的模拟:(1)来计算的驱动力gydF4y2Ba{\ \(\帽子σ}(t) \)gydF4y2Ba对应于任意动态变量gydF4y2Ba{\ \(\帽子varepsilon} (t) \)gydF4y2Ba;和(2),计算动态变量对应于一个已知的驱动力。在这两种情况下,我们必须考虑到限制gydF4y2Ba{\ \(\帽子varepsilon} (t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。gydF4y2Ba

目前的形式可以用于线性的非线性粘弹性材料,甚至为了测试范围的线性模型的有效性。的一些话题可以与形式主义研究大型振幅振荡剪切(老挝)获得流变测试gydF4y2Ba79年gydF4y2Ba和动态力学分析(DMA)从强迫共振分析仪和获得免费的共振分析仪gydF4y2Ba80年gydF4y2Ba。许多系统涉及的依赖与外部参数如频率或温度,看到例如参考文献。gydF4y2Ba81年gydF4y2Ba,gydF4y2Ba82年gydF4y2Ba,gydF4y2Ba83年gydF4y2Ba。这些系统不能进行直接的方式与目前的形式主义,看到“gydF4y2Ba讨论gydF4y2Ba”部分的更多细节。gydF4y2Ba

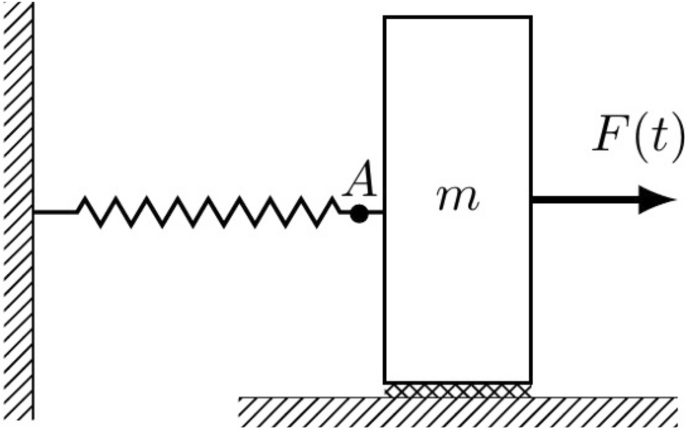
非线性阻尼gydF4y2Ba

图5gydF4y2Ba
图5gydF4y2Ba

图质量阻尼和弹性力。gydF4y2Ba

全尺寸图像gydF4y2Ba

考虑图的图。gydF4y2Ba5gydF4y2Ba)。身体质量gydF4y2Ba米gydF4y2Ba在接触表面阻尼力的贡献呢gydF4y2Ba\ (v b (v) \ \)gydF4y2Ba。外部的力量gydF4y2BaFgydF4y2Ba(gydF4y2BatgydF4y2Ba)应用于身体由弹簧连接到一个固定的墙。假设我们测量力点gydF4y2Ba一个gydF4y2Ba,例如通过使用应变计或负载细胞,系统的动力学方程gydF4y2Ba

$ $ \{对齐}开始F (t) -F_A b (t) = (v (t)) \;v (t) + m \;v (t), \{对齐}$ $gydF4y2Ba
(57)gydF4y2Ba

在哪里gydF4y2Ba\ \ (F_A (t))gydF4y2Ba力测量的点吗gydF4y2Ba一个gydF4y2Ba,gydF4y2BavgydF4y2Ba是身体的速度。通过比较情商。gydF4y2Ba57gydF4y2Ba)与情商。gydF4y2Ba1gydF4y2Ba),我们确定的驱动力gydF4y2Ba\ (y (t) = F (t) -F_A (t) \)gydF4y2Ba,动态变量gydF4y2Ba\ (x (t) = v (t) \)gydF4y2Ba和特性曲线gydF4y2Ba\ (f (x (t)) = b (v (t)) \; v (t) \)gydF4y2Ba和gydF4y2Ba\ (g (x (t)) = m \)gydF4y2Ba。系统建模是通过设置一个单音的动态变量gydF4y2Ba\ (v (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba并通过计算傅里叶分析的驱动力。一旦取得了特性曲线,我们可以模拟系统模拟的两种解释在无花果。gydF4y2Ba1gydF4y2Ba:(1)通过计算的驱动力gydF4y2Ba\(\帽子{F} (t) - {F_A} (t) \ \帽子)gydF4y2Ba对应于任意动态变量gydF4y2Ba\(\帽子}{v (t) \)gydF4y2Ba;(2)通过计算动态变量,对应于一个已知的驱动力。在这两种情况下,我们必须考虑到限制gydF4y2Ba\ (v (t) \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。gydF4y2Ba

注意,根据形式主义,大众可以依赖身体的速度。从实用的角度来看,我们可以添加这个假设的依赖gydF4y2Ba米gydF4y2Ba(gydF4y2BavgydF4y2Ba)和无花果的完整过程。gydF4y2Ba1gydF4y2Ba。后计算特性曲线gydF4y2BaggydF4y2Ba情商。gydF4y2Ba36gydF4y2Ba),预期的结果应该是一个常数。无论如何,如果有必要,我们可以力gydF4y2Ba米gydF4y2Ba是一个常数。这意味着我们可以计算特性曲线gydF4y2BafgydF4y2Ba根据情商。gydF4y2Ba36gydF4y2Ba),并设置gydF4y2Ba\ (g (x (t)) = m \)gydF4y2Ba系统仿真。根据gydF4y2Ba形式主义gydF4y2Ba部分,功能gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba是独立的,这意味着即使我们假设gydF4y2Ba\ (g (x (t)) = m \)gydF4y2Ba是一个常数,gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba)特性曲线不受影响。gydF4y2Ba

这个简单的例子让我们获得非线性阻尼力的非线性特性曲线,并使用它的系统仿真。提到是很重要的,我们需要在动态变量定下一个基调gydF4y2BavgydF4y2Ba(gydF4y2BatgydF4y2Ba)获得系统建模,这可能困难,实施在实际系统中,看到“gydF4y2Ba讨论gydF4y2Ba”部分的更多细节。尽管这个限制,可以适应这个简单的例子描述了一些潜在的应用在航空航天结构,微机电系统(MEMS)、非线性悬架和隔离系统gydF4y2Ba84年gydF4y2Ba,gydF4y2Ba85年gydF4y2Ba,gydF4y2Ba86年gydF4y2Ba。gydF4y2Ba

讨论gydF4y2Ba

线性微分方程可以通过统一的研究框架,如传递函数(TF)和频率响应函数(降维)工程或物理中的格林函数。在这些框架,第一谐波足以计算所有可能的线性行为。然而,对于非线性系统,高次谐波的存在是不可避免的。建模和求解非线性微分方程的统一框架仍在发展。接下来,我们提到的一些进步在这个方向和比较他们的形式工作。gydF4y2Ba

沃尔泰拉和维纳认为系列的输出是在以前的时间的输入值。此外,认为的NARMAX模型的输出是输入和输出值在先前的时候,前面和当前值函数的相关测量噪声。这个工作的形式主义在概念上不同于这些方法,而不是使用因为先前的值来预测下一个,它侧重于计算特性曲线定义系统的微分方程。在这个方向,我们使用所有输入输出的数据从一个完整的动态变量为了计算特性曲线的多项式回归模型只涉及动力学变量及其一阶导数。因此,该模型不使用以前的值以显式的方式。从概念上讲,以前的时候还取决于值的数量的方法用于计算一阶导数。如果一阶导数由一阶有限差分计算,我们只需要动态变量的值和前一个。然而,如果使用高阶微分方法,我们需要不止一个动态变量的前一个值。gydF4y2Ba

HBM, IBM和修改版本主要是基于非线性系统转化为一个代数方程的变换,分别为每个系统必须解决,例如,通过使用Newton-like方法或数值路径延续gydF4y2Ba87年gydF4y2Ba。这个工作的形式不同于这些方法主要是因为我们不使用显式定义的特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba在任何步骤的形式主义,这使我们能够事先操纵一阶方程解决问题,因此,情商。gydF4y2Ba36gydF4y2Ba)仍然有效的系统是基于一阶微分方程等情商。gydF4y2Ba1gydF4y2Ba)。这种形式主义,见补充M3,具有计算复杂度低,这使我们能够考虑到40次谐波,见补充M5,显著高于谐波中通常被认为是参考书目。值得一提的是,还需要更多的研究来阐明形式是否能够完全描述非线性共振现象,比如,周期和准周期振动,分岔和极限环,HBM和DFs的主要应用gydF4y2Ba88年gydF4y2Ba,gydF4y2Ba89年gydF4y2Ba。额外的考虑在本小节的末尾。gydF4y2Ba

的OFRFgydF4y2Ba49gydF4y2Ba,gydF4y2Ba50gydF4y2Ba,gydF4y2Ba51gydF4y2Ba和HOSIDFsgydF4y2Ba52gydF4y2Ba方法是重要贡献的研究基于频域非线性系统建模。这两种方法都提供了扩展的众所周知的特遣部队和降维的方法,广泛应用于线性系统理论、非线性系统。特别是OFRF提出了一种递归方法来获得一个非线性微分方程的系数傅里叶分析,这需要许多模拟和代数操作下的每个系统研究。HOSIDFs定义了一个虚拟谐波发生器和许多描述功能gydF4y2BangydF4y2Ba顺序,每个描述函数amplitude-dependent传递函数相关联。提出了工作的形式从OFRF和HOSIDFs方法在概念上是不同的,因为它不搜索TF的延伸和降维成非线性系统,相反,它旨在搜索直接傅里叶系数之间的关系,定义了非线性系统的特性曲线。通过使用这种方法,我们避免直接使用导出和虚拟谐波发电机,相反,我们事先操纵傅里叶级数来表示一个非线性一阶系统。尽管sirp法提出了工作是在概念上不同于OFRF和HOSIDFs方法,所有这些形式将以某种方式相关,这项工作可能被视为一种贡献为了定义一个统一的框架来研究非线性系统在频域。gydF4y2Ba

这个工作的形式直观的基于一个基本的结果从线性RL (RC)系统,在第一次谐波的振幅和相位的知识使我们能够找到的值R和L (R和C)。我们已经将这一概念扩展到非线性RL (RC)系统,通过傅里叶系数之间的等价的驱动力和多项式回归特性曲线的一阶微分方程。这个结果明确显示,傅里叶级数可以表示两个独立的非线性特性曲线gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba)。与平时相比这是一个不同的角度解释由傅里叶级数gydF4y2Ba\罪(\ \)gydF4y2Ba和gydF4y2Ba\ \因为\ ()gydF4y2Ba功能,形成一个正交有限域可数精确性的基础功能。这个角度看是一种形式主义的直接后果,并可能导致重新解释傅里叶级数的微分方程。此外,如补充M5所示,和根据gydF4y2Ba形式主义gydF4y2Ba部分,形式主义的实现提出了两个傅里叶和多项式回归的特点结合形式,因此龙格现象gydF4y2Ba90年gydF4y2Ba和Gibbs-Wilbraham现象gydF4y2Ba91年gydF4y2Ba,gydF4y2Ba92年gydF4y2Ba,gydF4y2Ba93年gydF4y2Ba同时存在。这些话可以是一个起点,产生进一步的研究方向。gydF4y2Ba

评论可以计算时间从补充M3。一方面,从FFT获得模型,计算的复杂性gydF4y2Ba\ (\ mathscr {O} (N \ ln) \)gydF4y2Ba74年gydF4y2Ba,在那里gydF4y2BaNgydF4y2Ba序列的长度吗gydF4y2Ba\(最大\)gydF4y2Ba。另一方面,仿真用情商。gydF4y2Ba36gydF4y2Ba)的计算复杂度gydF4y2Ba\ (\ mathscr {O} (N k_{马克斯}^ 2)\)gydF4y2Ba,这是gydF4y2Ba\ (\ mathscr {O} (N) \)gydF4y2Ba对于一个固定的gydF4y2Ba\ (k_{马克斯}\)gydF4y2Ba价值。由于这种低计算复杂度在两种建模与仿真,该技术有望适合实时应用程序,例如,在嵌入式系统中实现。此外,也可能是控制理论的一些形式主义的后果。gydF4y2Ba

限制可以涉及的范围动态变量,如果傅里叶系数计算通过使用一个动态变量gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba,这是限制范围gydF4y2Ba\ ([A_0-A_1 A_0 + A_1] \)gydF4y2Ba那么,其他动态变量gydF4y2Ba\ ({x} (t) \ \帽子)gydF4y2Ba用于模拟必须被限制在相同的范围。这种限制出现,因为傅里叶级数表示为一个幂级数展开,这提出了一个动态变量时散度gydF4y2Ba\ ({x} \ \帽子)gydF4y2Ba超出这个范围。gydF4y2Ba

另一个限制可能出现的一些真正的系统。过程中解释这项工作需要能够定下一个基调的动力学变量为了获得特性曲线。但对于一些实际系统由于设备限制或者只是由于限制在这个过程中,我们可能无法使用单个正弦语气获取特性曲线。进一步的研究可以解决为了克服这种限制。gydF4y2Ba

可以考虑关于这个形式主义一些真正的应用程序的系统特性曲线gydF4y2BafgydF4y2Ba和gydF4y2BaggydF4y2Ba这依赖于频率,即。gydF4y2Baf (x (t); \ \(ω)\)gydF4y2Ba和gydF4y2Ba\ (g (x (t); \ω)\)gydF4y2Ba,事实上,几乎所有的情况下材料在材料科学。这是简要地讨论了在应用程序中gydF4y2Ba非线性电感电容电阻测量计gydF4y2Ba。详细研究必须解决为了分析这个频率依赖的系统和的可能性被这里介绍的形式描述。我们讨论一些考虑在以下这个方向。考虑到频率相关特性曲线,我们可以添加gydF4y2Baω\ (\ \)gydF4y2Ba变量作为参数的特性曲线gydF4y2Baf (x (t); \ \(ω)\)gydF4y2Ba和gydF4y2Ba\ (g (x (t); \ω)\)gydF4y2Ba。此外,注意在形式主义,我们使用一个动态变量gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba获取系统建模,这意味着严格有效的非线性模型gydF4y2Baf (x (t); \ \(ω)\)gydF4y2Ba和gydF4y2Ba\ (g (x (t); \ω)\)gydF4y2Ba。是否改为动态变量gydF4y2Ba\(\帽子{x} (t) = A_1 \ sin(\帽子{\ω}t) + A_0 \)gydF4y2Ba,gydF4y2Ba\(ω\帽子{ω\}\ ne \ \)gydF4y2Ba那么,我们会严格获得另一个特性曲线gydF4y2Ba\ (f (x (t) \帽子{\ω})\)gydF4y2Ba和gydF4y2Ba\ (g (x (t) \帽子{\ω})\)gydF4y2Ba。这些特性曲线的差异预计将小的时候gydF4y2Ba\(\帽子{ω\}\)gydF4y2Ba接近gydF4y2Baω\ (\ \)gydF4y2Ba和更大的遥远。如果我们考虑一系列的频率gydF4y2Ba\ω_i (\ \)gydF4y2Ba与gydF4y2Ba\(我在(1,n) \ \)gydF4y2Ba动态变量,然后我们将能够应用每个频率的形式获得一组特性曲线{gydF4y2Ba\ (f_i (x (t) \ω_i), g_i (x (t) \ω_i) \)gydF4y2Ba},gydF4y2Ba\(我在(1,n) \ \)gydF4y2Ba,每个模型是有效的一系列围绕其对应的频率。提到很重要的特性曲线得到这项工作时动态变量是一个单音。如果频率特性曲线不依赖,我们可以确保一个任意的驱动力模型是有效的,特别是它是有效的单音。然而,在频率相关特性曲线的情况下有一个额外的问题解决,可以制定为:对于一个给定的单音的驱动力,是动态变量的频率存在吗?。这是一个简单的问题,可能在将来的工作中得到解决。此外,大多数的材料也取决于与其他外部参数,如温度和功耗。形式主义没有考虑这些影响,并进一步研究可能是为了调查包括他们。gydF4y2Ba

最后,需要进一步的研究来阐明如果形式能够完全代表等复杂现象分岔,磁滞效应,以及其他一些重要的现象,在本质上与第二或高阶微分方程,如混沌动力系统gydF4y2Ba94年gydF4y2Ba和非线性共振gydF4y2Ba95年gydF4y2Ba。gydF4y2Ba

结论gydF4y2Ba

找到明确的证据之间的等价傅里叶分析的驱动力gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)和多项式回归的特性曲线gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba为一阶系统)gydF4y2Ba\ (y (t) = f (x (t)) + g (x (t)) \, x (t) \)gydF4y2Ba。这个工作让我们获得的表达式基于正弦动态系统建模变量gydF4y2Ba\ (x (t) = A_1 \罪(\ωt) + A_0 \)gydF4y2Ba的傅里叶分析和其相应的驱动力gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)。模型由傅里叶系数gydF4y2Ba\ (a_k \)gydF4y2Ba和gydF4y2Ba\ (b_k \)gydF4y2Ba和的值gydF4y2Ba\ (A_0 \)gydF4y2Ba,gydF4y2Ba\ (A_1 \)gydF4y2Ba和gydF4y2Ba\ (A_1 ' =ωA_1 \ \)gydF4y2Ba。然后,这个模型可以用于时域仿真与限制gydF4y2Ba\(\帽子{x} \ [A_0-A_1 A_0 + A_1] \)gydF4y2Ba。在电路理论的语言,gydF4y2BafgydF4y2Ba(gydF4y2BaxgydF4y2Ba),gydF4y2BaggydF4y2Ba(gydF4y2BaxgydF4y2Ba)对应于电阻和电抗非线性元素,分别。因此,本文提供的形式让我们与驱动力的傅里叶分析这两个特性曲线的非线性元素。特性曲线依赖于一组不同的傅里叶系数,这使我们能够独立识别每个函数。gydF4y2Ba

实际实现的方法是基于变量gydF4y2BaxgydF4y2Ba(gydF4y2BatgydF4y2Ba),gydF4y2BaygydF4y2Ba(gydF4y2BatgydF4y2Ba)通常是由采样序列{gydF4y2Ba\ (x_n \)gydF4y2Ba},{gydF4y2Ba\(最大\)gydF4y2Ba},gydF4y2Ba在[0,n - 1] \ (n \ \)gydF4y2Ba,这让我们获得FFT的傅里叶系数,因此,整个方法计算复杂度对实时应用程序的足够小。此外,形式主义让我们考虑一个更高的谐波比通常报道的系统建模。提出了一些示范例子通过考虑到40年代谐波。gydF4y2Ba