通过控制一小部分节点来维持网络gydF4y2Ba

生物、社会或技术的复杂系统，在某些情况下，会经历灾难性的故障，导致整个系统功能的崩溃。例如，电力系统的过载故障gydF4y2Ba^{1gydF4y2Ba，gydF4y2Ba2gydF4y2Ba}在生态网络中，物种灭绝gydF4y2Ba^{3.gydF4y2Ba，gydF4y2Ba4gydF4y2Ba，gydF4y2Ba5gydF4y2Ba}在一个城市，交通堵塞gydF4y2Ba^6gydF4y2Ba，细胞动力学中的细胞死亡gydF4y2Ba^{7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba}．这种崩溃可能是由结构损坏引起的，导致网络失去连通性gydF4y2Ba^{9gydF4y2Ba，gydF4y2Ba10gydF4y2Ba，gydF4y2Ba11gydF4y2Ba，gydF4y2Ba12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba，gydF4y2Ba14gydF4y2Ba，gydF4y2Ba15gydF4y2Ba}．然而，由于稀疏连接和/或功能干扰，一些系统可能会失去它们的功能，尽管它们仍然连接gydF4y2Ba^{16gydF4y2Ba，gydF4y2Ba17gydF4y2Ba，gydF4y2Ba18gydF4y2Ba，gydF4y2Ba19gydF4y2Ba，gydF4y2Ba20.gydF4y2Ba，gydF4y2Ba21gydF4y2Ba，gydF4y2Ba22gydF4y2Ba，gydF4y2Ba23gydF4y2Ba，gydF4y2Ba24gydF4y2Ba，gydF4y2Ba25gydF4y2Ba，gydF4y2Ba26gydF4y2Ba，gydF4y2Ba27gydF4y2Ba}．一旦一个系统崩溃，问题是它如何应对这种情况。可以区分两种类型的系统。有些系统可以自行恢复并恢复到正常的功能状态，而另一些系统则保持异常的非活动状态，只能通过外部恢复来恢复。前者被认为是“可持续的”系统，因为它们即使在受到干扰后也能永久地活动。相反，后一种类型被认为是“不可持续的”系统，因为即使它们是稳定的，但在外部扰动的存在下，它们也会崩溃，不会自发地恢复到原始状态。事实上，这两种类型之间的区别，是动力学的双稳定性特征gydF4y2Ba^21gydF4y2Ba．如果有另一种稳定状态，无功能状态，那么一旦系统达到这个状态它就会保持这个状态。然而，当活跃状态是唯一的稳定状态时，就没有陷入另一个稳定状态的危险，因为没有这样的稳定状态。gydF4y2Ba

从可控理论等角度探讨了控制节点活动的影响gydF4y2Ba^{28gydF4y2Ba，gydF4y2Ba29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba}，小扰动在网络中的传播模式gydF4y2Ba^{31gydF4y2Ba，gydF4y2Ba32gydF4y2Ba，gydF4y2Ba33gydF4y2Ba}，以及对系统状态的全局影响gydF4y2Ba^{34gydF4y2Ba，gydF4y2Ba35gydF4y2Ba，gydF4y2Ba36gydF4y2Ba，gydF4y2Ba37gydF4y2Ba，gydF4y2Ba38gydF4y2Ba}．最近的一项研究gydF4y2Ba^39gydF4y2Ba已经表明，对于某些系统，在某些条件下，即使控制一个“单一”节点也可以将整个系统移动到所需的系统自然活动状态。当控制信号设法围绕源单个节点从一个shell传播到另一个shell时，就会发生这种情况，就像多米诺骨牌效应一样，以创建“宏观”影响。然而，对于其他系统或在不同条件下，微观干预只能产生人们所期望的局部“微观”效应。当出现这种情况时，就需要宏观干预来创造一个全球性的变化。然而，一个基本的问题是，宏观控制导致的系统状态的全局变化是否只是定量的，甚至可以是定性的，即消除了较低的状态，如果是这样，需要控制的节点的比例是多少。gydF4y2Ba

在本研究中，我们旨在通过支持部分节点的活动来探索将不可持续系统转化为可持续系统的问题。我们讨论的干预是通过强制分数来完成的gydF4y2BaρgydF4y2Ba的受控节点具有较高的活动值Δ。我们开发了一个框架来预测给定的网络结构和给定的干预(由gydF4y2BaρgydF4y2Ba以及Δ)，前提是该系统变得可持续。通过定义一个参数gydF4y2BaβgydF4y2Ba^25gydF4y2Ba，以捕捉网络的连通性，我们在(gydF4y2BaβgydF4y2Ba，gydF4y2BaρgydF4y2Ba)空间。从这个相图中，对于一个给定的网络具有一定的gydF4y2BaβgydF4y2Ba，我们可以确定节点的最小(临界)分数gydF4y2BaρgydF4y2Ba_cgydF4y2Ba这是维持网络所必需的。从另一个角度来看，我们也可以确定，对于一个给定的可控制的分数(gydF4y2BaρgydF4y2Ba)，即网络的连接程度应如何才能持续发展。我们发现，与控制单个节点相比，通过控制一小部分节点，我们大大扩大了“可持续阶段”gydF4y2Ba^39gydF4y2Ba．我们进一步提出了一个理论，该理论连接了宏观和微观强迫节点集的两个极限，涵盖了两个极端以及介于两者之间的范围。我们演示并应用我们的框架到三个动态过程，细胞，神经元和自旋动力学，显示其普遍性。然而，不同的系统表现出明显不同的维持相图。gydF4y2Ba

不可持续的网络gydF4y2Ba

为了找到网络不可持续的条件，我们首先分析一个没有外部干预的自由系统的动力学。我们依赖一个总的框架gydF4y2Ba^{31gydF4y2Ba，gydF4y2Ba32gydF4y2Ba，gydF4y2Ba33gydF4y2Ba}建立网络的非线性动力学模型。考虑一个由gydF4y2BaNgydF4y2Ba组件(节点)，其活动gydF4y2BaxgydF4y2Ba_我gydF4y2Ba（gydF4y2Ba我gydF4y2Ba= 1,2，…，gydF4y2BaNgydF4y2Ba)关注Barzel-BarabásigydF4y2Ba^31gydF4y2Ba方程,gydF4y2Ba

第一个函数，gydF4y2Ba米gydF4y2Ba_0gydF4y2Ba（gydF4y2BaxgydF4y2Ba_我gydF4y2Ba)，捕获节点gydF4y2Ba我gydF4y2Ba的自我动力学，描述蛋白质降解等机制gydF4y2Ba^40gydF4y2Ba(细胞)，个体恢复gydF4y2Ba^{41gydF4y2Ba，gydF4y2Ba42gydF4y2Ba}(流行病)，或出生/死亡过程gydF4y2Ba^43gydF4y2Ba(人口动态)。该产品gydF4y2Ba米gydF4y2Ba_1gydF4y2Ba（gydF4y2BaxgydF4y2Ba_我gydF4y2Ba）gydF4y2Ba米gydF4y2Ba_2gydF4y2Ba（gydF4y2BaxgydF4y2Ba_jgydF4y2Ba)描述gydF4y2Ba我gydF4y2Ba，gydF4y2BajgydF4y2Ba相互作用机制，例如基因激活gydF4y2Ba^{7gydF4y2Ba，gydF4y2Ba44gydF4y2Ba，gydF4y2Ba45gydF4y2Ba}、感染gydF4y2Ba^{41gydF4y2Ba，gydF4y2Ba42gydF4y2Ba}或共生关系gydF4y2Ba^46gydF4y2Ba．二进制邻接矩阵gydF4y2Ba一个gydF4y2Ba捕获网络，即节点之间的交互(链接)。一个元素gydF4y2Ba一个gydF4y2Ba_{我gydF4y2BajgydF4y2Ba}如果节点之间存在交互(链接)，则等于1gydF4y2Ba我gydF4y2Ba而且gydF4y2BajgydF4y2Ba否则为0。矩阵gydF4y2Ba一个gydF4y2Ba是对称的，并遵守配置模型的特征。相互作用的强度由正参数决定gydF4y2BaλgydF4y2Ba．gydF4y2Ba

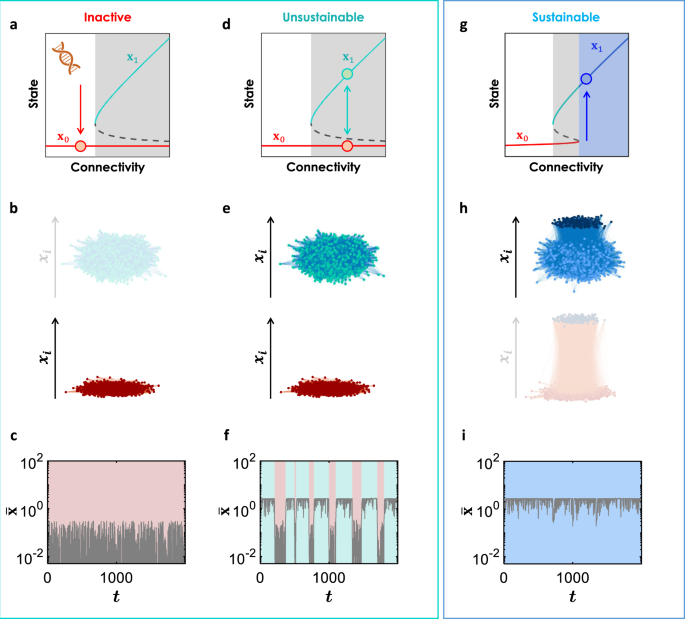
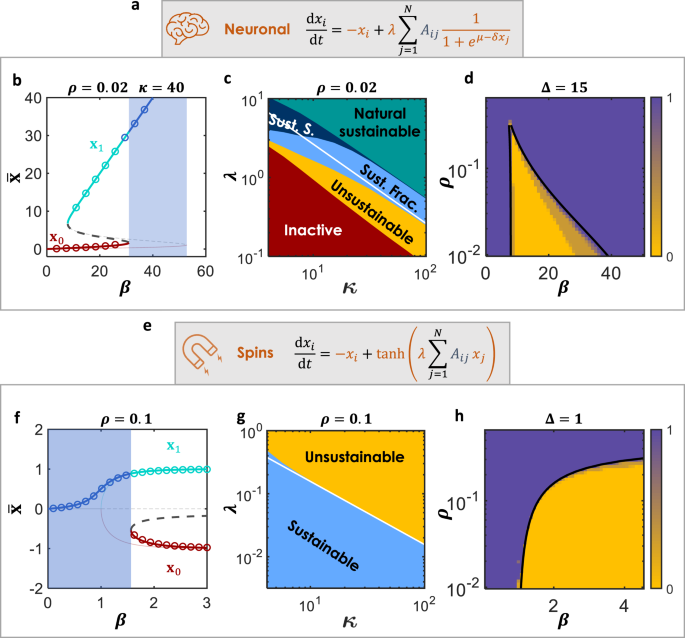
在无花果。gydF4y2Ba1gydF4y2Ba，我们在基因调控动力学的例子上演示了我们的问题，下面将详细探讨和介绍。对于弱连通性，表现为相互作用强度低或链接密度小，只存在所有基因都被抑制的低活性状态，如图。gydF4y2Ba1gydF4y2BaA, b，而对于强连通性，会出现额外的高活性状态。然而，低活跃状态仍然存在，图。gydF4y2Ba1gydF4y2Bad, e，它允许由于一些干扰而导致从功能性崩溃为非功能性的风险，见图。gydF4y2Ba1gydF4y2Baf.因此，这种活跃状态被称为不可持续状态，因为它有可能无法进入非活跃状态。在这项研究中，我们展示了如何支持一小部分系统节点(图2)。gydF4y2Ba1gydF4y2Bag, h，深蓝色)消除了非功能状态，从而使系统对扰动具有可持续性，图。gydF4y2Ba1gydF4y2Ba我。gydF4y2Ba

维系人际网络gydF4y2Ba

为了让一个不可持续的网络变得可持续，我们考虑了一个简单的干预措施。我们强制一组节点gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba(分数gydF4y2BaρgydF4y2Ba)具有恒定的高活性值Δ(图;gydF4y2Ba1gydF4y2BaH)，其余的都在互补集中gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba都是由原始动力控制的。因此，这样一个受迫系统服从于下列方程组，gydF4y2Ba

虽然在某些系统中，如此简单的干预是一项技术挑战，但我们认为这是一个原型案例，从中我们可以推断出其他案例。例如，如果一个恒定的控制高度Δ起作用，那么我们可以保持被控制节点的活动高于Δ或等于Δ，以维持系统。其他干预措施，如添加流量，可以等效地转换为用由流量引起的新的稳定值保持节点的活动。如果我们回到上面的基因调控的例子，基因表达的操纵是一种常见的做法，例如，使用光gydF4y2Ba^47gydF4y2Ba．gydF4y2Ba

接下来，我们的目标是跟踪非强制节点(即集合)的状态gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba．为了找到强制系统的稳态，我们要求松弛，这样导数就消失了。此外，我们使用了基于程度的平均场近似gydF4y2Ba^{42gydF4y2Ba，gydF4y2Ba48gydF4y2Ba，gydF4y2Ba49gydF4y2Ba，gydF4y2Ba50gydF4y2Ba，gydF4y2Ba51gydF4y2Ba}假设具有相同度的节点行为相似。因此，我们替换了二进制项gydF4y2Ba一个gydF4y2Ba_{我gydF4y2BajgydF4y2Ba}与概率之间存在联系gydF4y2Ba我gydF4y2Ba而且gydF4y2BajgydF4y2Ba在构型模型中，gydF4y2BakgydF4y2Ba_我gydF4y2BakgydF4y2Ba_jgydF4y2Ba／（gydF4y2BaNgydF4y2Ba〈gydF4y2BakgydF4y2Ba>) wheregydF4y2BakgydF4y2Ba_我gydF4y2Ba而且gydF4y2BakgydF4y2Ba_jgydF4y2Ba是度gydF4y2Ba我gydF4y2Ba而且gydF4y2BajgydF4y2Ba,分别。考虑到这一点，我们将order参数Θ定义为(参见Section Methods中的详细说明)gydF4y2Ba

表示任意自由节点从其任意自由邻居获得的平均影响。的变量gydF4y2Ba\ ({x} _ {j} ^ {*} \)gydF4y2Ba表示节点的活动gydF4y2BajgydF4y2Ba在放松中，和gydF4y2Ba\({{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba表示只计算其中的链接gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba，即非受迫节点。使用已定义的Θ，并应用Eq. (gydF4y2Ba2gydF4y2Ba)在松弛中，我们得到，gydF4y2Ba

在哪里gydF4y2BaRgydF4y2Ba（gydF4y2BaxgydF4y2Ba) =−gydF4y2Ba米gydF4y2Ba_0gydF4y2Ba（gydF4y2BaxgydF4y2Ba）/gydF4y2Ba米gydF4y2Ba_1gydF4y2Ba（gydF4y2BaxgydF4y2Ba),gydF4y2Ba\ ({k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}\)gydF4y2Ba强制邻居的数量(ingydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba节点的)gydF4y2Ba我gydF4y2Ba哪个是自由动态节点(在gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba)．将其代入Θ的定义中，我们得到了一个自洽的顺序参数方程，gydF4y2Ba

在哪里gydF4y2BaRgydF4y2Ba^{−1gydF4y2Ba}的逆函数是gydF4y2BaRgydF4y2Ba．这一步假设gydF4y2BaRgydF4y2Ba是可逆函数。求解自洽方程(gydF4y2Ba5gydF4y2Ba)，我们得到了系统的所有状态(稳定和不稳定)。这个方程可以用任意的度分布和节点的特定选择来求解gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba(参见章节方法)。gydF4y2Ba

得到，除了Eq. (gydF4y2Ba5gydF4y2Ba)，更直观，简单和有用的表达式，我们假设以下额外的近似基于一个常见的平均场(MF)方法。当度分布不是很宽的时候和/或函数gydF4y2Ba米gydF4y2Ba_2gydF4y2Ba而且gydF4y2BaRgydF4y2Ba是接近线性还是常数，我们把平均值插入函数中gydF4y2Ba^25gydF4y2Ba,也就是说,gydF4y2Ba\(\眉题{{M} _ {2 }({{{{{{{\ 男朋友{x }}}}}}}})}={ M} _{2}(\酒吧{{{{{{{{\ bf {x }}}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\ \眉题{R ({{{{{{{\ bf {x }}}}}}}})}= R(\酒吧{{{{{{{{\ bf {x }}}}}}}}})\)gydF4y2Ba，得到前导阶的近似值，请参见Section方法。这允许我们使用等式。（gydF4y2Ba3.gydF4y2Ba)及(gydF4y2Ba4gydF4y2Ba)，得到一个非常简单的平均稳态之间的关系gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba自由节点和连通性gydF4y2BaβgydF4y2Ba的网络为一个给定的控件，其特征为gydF4y2BaρgydF4y2BaΔ。我们定义平均活动gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba胜过所有的邻居gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba通过gydF4y2Ba

还有连接性gydF4y2BaβgydF4y2Ba定义为gydF4y2Ba

结合两种相互作用的强度gydF4y2BaλgydF4y2Ba而整个网络的平均邻居度，gydF4y2BaκgydF4y2Ba= kgydF4y2Ba^2gydF4y2Ba〉/〈gydF4y2BakgydF4y2Ba〉.利用这些项，我们最终得到了一个关于受迫系统状态的简单方程，为gydF4y2BaκgydF4y2Ba≫gydF4y2Ba1和随机选择强制节点，gydF4y2Ba

在哪里gydF4y2Ba\(\rho =| {{{{{{{\mathcal{F}}}}}}}}| /N\)gydF4y2Ba是被控制节点的分数。为了得到自由系统的状态，我们可以代入gydF4y2BaρgydF4y2Ba= 0，屈服gydF4y2Ba\ \β= R(\酒吧{{{{{{{{\ bf {x }}}}}}}}})/{ M} _{2}(\酒吧{{{{{{{{\ bf {x }}}}}}}}})\)gydF4y2Ba．(对于强制节点的非随机选择，而是依赖于程度的选择，请参见补充说明gydF4y2Ba2gydF4y2Ba．）gydF4y2Ba

情商。gydF4y2Ba8gydF4y2Ba)意味着强制一个分数gydF4y2BaρgydF4y2Ba有一个gydF4y2BaxgydF4y2Ba_我gydF4y2Ba-value Δ更改系统的相位图，并为强制系统创建新的相位图。为了证明相图中的这种变化，我们回到基因调控的主要例子。应用图中的一般方程。gydF4y2Ba2gydF4y2Baa对基因调控产生的自由系统，图。gydF4y2Ba2gydF4y2BaB，显示两个政权:弱连通性的不活跃状态，和一个双稳定政权(灰色阴影)以上的一定gydF4y2BaβgydF4y2Ba．与此形成鲜明对比的是，强制体系的相图明显不同。gydF4y2Ba2gydF4y2BaC，表现为三种状态:不活跃为小gydF4y2BaβgydF4y2Ba，为中间体双稳定性gydF4y2BaβgydF4y2Ba的某一值以上gydF4y2BaβgydF4y2Ba只有活动状态。神经元和自旋动力学，图。gydF4y2Ba2gydF4y2BaD-g，具有不同的相图，通过控制系统的一小部分也会发生变化。gydF4y2Ba

在这三个例子中，位于双稳定区域(灰色阴影)内的高活性状态的自由系统被认为是不可持续的。这是因为存在一种潜在的不活跃状态。但是，控制一个分数gydF4y2BaρgydF4y2Ba对于具有高活性的节点Δ，将重新塑造相图并创建一个区域(蓝色阴影)，在该区域中，系统变得更安全，也就是说，没有进入低状态的故障风险。因此，该系统变得可持续。gydF4y2Ba

应用:细胞动力学gydF4y2Ba

作为本文的主要示例，我们应用了根据Michaelis-Menten模型捕获的调控动态框架gydF4y2Ba^44gydF4y2Ba,通过gydF4y2Ba

在这个框架下，gydF4y2Ba\ ({M} _ {0} ({x} _{我})= - b {x} _{我}^ {}\)gydF4y2Ba，描述退化(gydF4y2Ba一个gydF4y2Ba= 1)，二聚体(gydF4y2Ba一个gydF4y2Ba= 2)或更复杂的生化消耗过程(分数gydF4y2Ba一个gydF4y2Ba)，以一定的速度发生gydF4y2BaBgydF4y2Ba；不失一般性，我们设在这里gydF4y2BaBgydF4y2Ba= 1。激活相互作用由表单的Hill函数捕获gydF4y2Ba米gydF4y2Ba_1gydF4y2Ba（gydF4y2BaxgydF4y2Ba_我gydF4y2Ba) = 1，gydF4y2Ba\ ({M} _ {2} ({x} _ {j}) = {x} _ {j} ^ {h} / (1 + {x} _ {j} ^ {h}) \)gydF4y2Ba，一个类似开关的功能，饱和到gydF4y2Ba米gydF4y2Ba_2gydF4y2Ba（gydF4y2BaxgydF4y2Ba_jgydF4y2Ba→1表示大gydF4y2BaxgydF4y2Ba_jgydF4y2Ba,代表gydF4y2BajgydF4y2Ba的正的，尽管有界的，对节点的贡献gydF4y2Ba我gydF4y2Ba活动,gydF4y2BaxgydF4y2Ba_我gydF4y2Ba（gydF4y2BatgydF4y2Ba)．gydF4y2Ba

当分析这个方程组时，它被一个分数强制gydF4y2BaρgydF4y2Ba活动为Δ的随机节点的，则利用式(gydF4y2Ba8gydF4y2Ba)，gydF4y2Ba

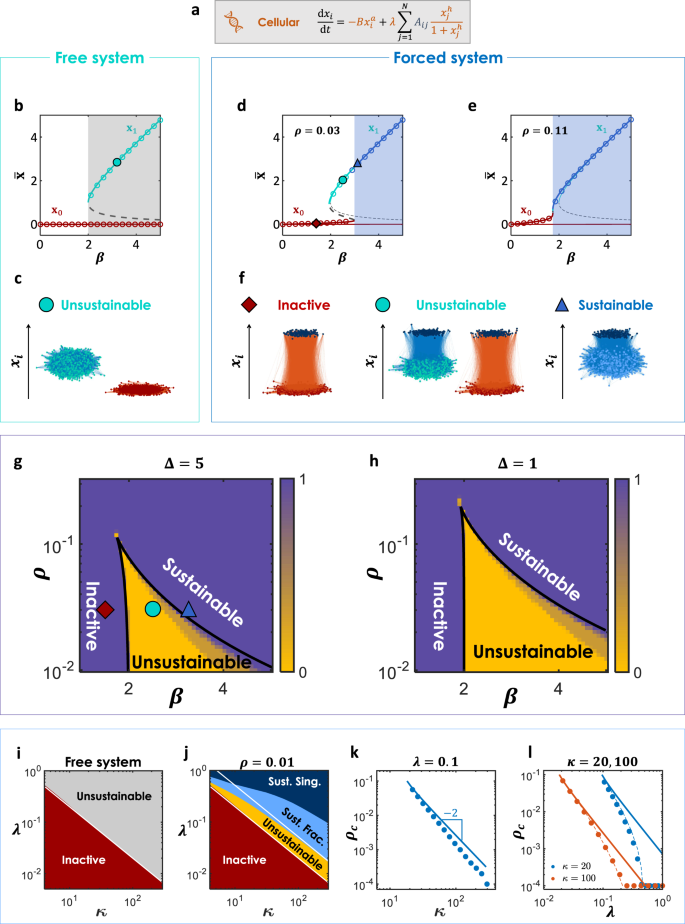
在无花果。gydF4y2Ba3.gydF4y2Ba，我们详细介绍了在设置时使用模拟和理论的细胞动力学结果gydF4y2Ba一个gydF4y2Ba= 1,gydF4y2BahgydF4y2Ba= 2。自由系统的相图，由式(gydF4y2Ba10gydF4y2Ba)代入gydF4y2BaρgydF4y2Ba= 0，如图所示。gydF4y2Ba3.gydF4y2Bab.注意gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}= 0 \)gydF4y2Ba自由系统的稳定状态，不是通过代入得到的吗gydF4y2BaρgydF4y2Ba式中= 0 (gydF4y2Ba10gydF4y2Ba)，但由MF方程，见补充注gydF4y2Ba1gydF4y2Ba．然而，它也可以由式(gydF4y2Ba10gydF4y2Ba)求极限gydF4y2BaρgydF4y2Ba→0。如上所述，高活性状态gydF4y2BaxgydF4y2Ba_1gydF4y2Ba在整个范围内都是不可持续的，如图所示。gydF4y2Ba3.gydF4y2Bac. Eq. (gydF4y2Ba10gydF4y2Ba)还可生成如图所示的强制系统的相图。gydF4y2Ba3.gydF4y2BaD(粗曲线)为gydF4y2BaρgydF4y2Ba= 0.03和Δ = 5，显示了一个s形图，现在也有一个新的只活跃的区域(蓝色阴影)。这一制度处于可持续发展阶段。在无花果。gydF4y2Ba3.gydF4y2BaF，我们展示了三种不同状态下的强迫系统状态，并表明gydF4y2BaβgydF4y2Ba= 3.1时，图中外部干预使系统可持续而非不可持续。gydF4y2Ba3.gydF4y2Bac.图中显示了低状态消失的含义。gydF4y2Ba1gydF4y2BaF, i，其中，相对于不受控制的不可持续系统，受支持系统对于大的随机扰动是可持续的。注意，该控件还增加了高状态的级别，gydF4y2BaxgydF4y2Ba_1gydF4y2Ba，但这种影响很小。s形，图。gydF4y2Ba3.gydF4y2BaD，揭示了的临界值gydF4y2BaβgydF4y2Ba=gydF4y2BaβgydF4y2Ba_cgydF4y2Ba在此之上，系统是可持续的。这gydF4y2BaβgydF4y2Ba_cgydF4y2Ba取决于gydF4y2BaρgydF4y2Ba，这个关系在相反的方向上也成立，即，对于给定gydF4y2BaβgydF4y2Ba有一个必要的临界分数gydF4y2BaρgydF4y2Ba_cgydF4y2Ba控制节点，使系统可持续。的临界值之间的关系gydF4y2BaρgydF4y2Ba而且gydF4y2BaβgydF4y2Ba在从双稳定区域过渡到可持续阶段和非活跃区域时。从图中可以看出。gydF4y2Ba3.gydF4y2BaD，两个过渡都是的局部极值gydF4y2Ba\ \β(\酒吧{{{{{{{{\ bf {x }}}}}}}}})\)gydF4y2Ba，因此用式(gydF4y2Ba8gydF4y2Ba)gydF4y2Ba

情商。gydF4y2Ba11gydF4y2Ba)提供gydF4y2BaβgydF4y2Ba_cgydF4y2Ba作为两个分数的函数gydF4y2BaρgydF4y2Ba和控制的力量Δ。使用Eq. (gydF4y2Ba10gydF4y2Ba)我们得到gydF4y2BaβgydF4y2Ba_cgydF4y2Ba或gydF4y2BaρgydF4y2Ba_cgydF4y2Ba细胞动力学。对于基因调控而言，解决之道并非琐碎(见方法)，但在限度小gydF4y2BaρgydF4y2Ba，当我们得到一个很小的值gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba在过渡处，如图所示。gydF4y2Ba3.gydF4y2BaD，得到标度关系，gydF4y2Ba

的确，在我们的模拟中，对于这些值，gydF4y2Ba一个gydF4y2Ba= 1,gydF4y2BahgydF4y2Ba= 2，由图可知。gydF4y2Ba3.gydF4y2Bak,gydF4y2BaρgydF4y2Ba_cgydF4y2Ba~gydF4y2BaβgydF4y2Ba^{−2gydF4y2Ba},在那里gydF4y2BaβgydF4y2Ba=gydF4y2BaλgydF4y2BaκgydF4y2Ba．我们将在下面进一步讨论这个结果。gydF4y2Ba

数字gydF4y2Ba3.gydF4y2BaE显示的结果与gydF4y2Ba3.gydF4y2BaD表示较大比例的受控节点，gydF4y2BaρgydF4y2Ba= 0.11。我们可以看到这个值gydF4y2BaρgydF4y2Ba时，双稳定区几乎完全消失。这意味着另一个临界分数gydF4y2BaρgydF4y2Ba_0gydF4y2Ba，超过此值，系统的活动状态对任何都是可持续的gydF4y2BaβgydF4y2Ba．为了找到这个gydF4y2BaρgydF4y2Ba_0gydF4y2Ba时，我们注意到它捕获了局部极大值和最小值的合并，因此除了Eq. (gydF4y2Ba11gydF4y2Ba)时，二阶导数也应消失，gydF4y2Ba

这两个条件，等式。（gydF4y2Ba11gydF4y2Ba)及(gydF4y2Ba13gydF4y2Ba)，共同决定一个临界点(gydF4y2BaβgydF4y2Ba_0gydF4y2Ba，gydF4y2BaρgydF4y2Ba_0gydF4y2Ba)在(gydF4y2BaβgydF4y2Ba，gydF4y2BaρgydF4y2Ba)，在这个空间，三个阶段:不活跃、不可持续和可持续相遇，超过这个空间，系统将根本不会经历突变，见图。gydF4y2Ba3.gydF4y2Bag。gydF4y2Ba

对于细胞动力学，我们发现(见方法)，gydF4y2Ba

为了我们的价值观gydF4y2Ba一个gydF4y2Ba= 1,gydF4y2BahgydF4y2Ba= 2，对于较大的Δ，大约等于1/9，而使用Δ = 1时，它得到一个更高的1/5值，见图。gydF4y2Ba3.gydF4y2Bag h。gydF4y2Ba

在无花果。gydF4y2Ba3.gydF4y2BaG, h，我们在(gydF4y2BaβgydF4y2Ba，gydF4y2BaρgydF4y2Ba)-用于网络的空间gydF4y2BaκgydF4y2Ba= 20,60,100显示出良好的协议之间的模拟和理论，等式。（gydF4y2Ba10gydF4y2Ba)及(gydF4y2Ba11gydF4y2Ba)．注意，正如预期的那样，对于更大的gydF4y2BaκgydF4y2Ba，理论与模拟结果吻合较好。此外，可以看出临界点与式一致(gydF4y2Ba14gydF4y2Ba)，并且对于较小的Δ，它会变得更高，图。gydF4y2Ba3.gydF4y2Bah.图中的符号。gydF4y2Ba3.gydF4y2Bag指图中的演示。gydF4y2Ba3.gydF4y2BaF显示每个区域的系统状态。gydF4y2Ba

接下来，我们拆分合并的连接性gydF4y2BaβgydF4y2Ba移动到三维空间(gydF4y2BaκgydF4y2Ba，gydF4y2BaλgydF4y2Ba，gydF4y2BaρgydF4y2Ba)，特别是在(gydF4y2BaκgydF4y2Ba，gydF4y2BaλgydF4y2Ba)讨论。这是因为我们也想测试低阶的系统行为，因此我们进行了解耦gydF4y2BaβgydF4y2Ba分成两个参数gydF4y2BaκgydF4y2Ba而且gydF4y2BaλgydF4y2Ba， Eq. (gydF4y2Ba7gydF4y2Ba)．此外，我们希望推广相图，以包括单节点恢复模型gydF4y2Ba^39gydF4y2Ba在一定条件下，控制一个节点可以使整个系统恢复到高活跃状态。当它工作时，它也使系统可持续，因为它取消了低活跃状态。数字gydF4y2Ba3.gydF4y2Bai为上图中有两个区域的自由系统相图。gydF4y2Ba3.gydF4y2Bab.图。gydF4y2Ba3.gydF4y2BaJ，我们显示的是组合单节点复活(深蓝色)和分数复活gydF4y2BaρgydF4y2Ba= 0.01(浅蓝色)。对系统一小部分的控制大大延长了可持续阶段。白线代表我们的理论结果，通过计算gydF4y2BaβgydF4y2Ba_cgydF4y2Ba用方程式。（gydF4y2Ba10gydF4y2Ba)及(gydF4y2Ba11gydF4y2Ba)．请注意，该理论适用于高gydF4y2BaκgydF4y2BaWhile为小值偏离。原因在于平均场近似的性质，它通常只在很大程度上在定量上起作用。原因是，如果节点有更多的邻居，那么不同的邻居就会更相似，就像平均场理论所假设的那样。gydF4y2Ba

在无花果。gydF4y2Ba3.gydF4y2BaK，我们穿过(gydF4y2BaκgydF4y2Ba，gydF4y2BaλgydF4y2Ba)-空间水平为固定gydF4y2BaλgydF4y2Ba= 0.1gydF4y2BaκgydF4y2Ba．符号代表模拟，直线代表理论，由等式得到。（gydF4y2Ba10gydF4y2Ba)及(gydF4y2Ba11gydF4y2Ba)．这支持式(gydF4y2Ba12gydF4y2Ba）gydF4y2BaρgydF4y2Ba_cgydF4y2Ba~gydF4y2BaβgydF4y2Ba^{−2gydF4y2Ba}．见图。gydF4y2BaS3gydF4y2Ba对于其他值gydF4y2Ba一个gydF4y2Ba而且gydF4y2BahgydF4y2Ba．可见，对于很小的人来说gydF4y2BaρgydF4y2Ba尽管如此，偏差还是在增加gydF4y2BaκgydF4y2Ba很大。这种微小的差异在图中变得更大。gydF4y2Ba3.gydF4y2BaL，垂直移动gydF4y2BaλgydF4y2Ba固定gydF4y2BaκgydF4y2Ba= 20 andgydF4y2BaκgydF4y2Ba= 100。这里的理论偏差(连续线)为小gydF4y2BaρgydF4y2Ba是显著的。然而，正如预期的那样，学位越高，情况就越好。这一差距暴露了我们的MF和关于极限的模拟之间的矛盾gydF4y2BaρgydF4y2Ba→0，如下所述。gydF4y2Ba

的极限gydF4y2BaρgydF4y2Ba→0gydF4y2Ba

我们的MF理论，根据定义，得出了这个结论gydF4y2BaρgydF4y2Ba→0推导gydF4y2BaβgydF4y2Ba_cgydF4y2Ba→gydF4y2Ba∞gydF4y2Ba就像一个完全没有干预的自由系统。然而，它已经被证明了gydF4y2Ba^39gydF4y2Ba足够大了gydF4y2BaλgydF4y2Ba即使是单个节点也会对整个网络产生影响。MF函数在很小的时候失效的原因gydF4y2BaρgydF4y2Ba而不是很大的度数(见图中的连续线)。gydF4y2Ba3.gydF4y2Bal)当只有一个或几个受控节点时，MF所依赖的网络中不同节点的均匀性或同质性假设被打破。该网络得到一个围绕少数受控节点的壳层结构，如参考文献中所分析的。gydF4y2Ba^39gydF4y2Ba．因此，我们在这里提出了一种改进的壳层MF，它也包括许多受控节点的情况，而不是只有一个。这种方法跨越了微观和宏观干预的界限。它涉及分析和计算部分的组合，以覆盖边缘和中间范围。一个完整的解析解仍有待得到。参见补充说明gydF4y2Ba3.gydF4y2Ba获取详细信息。图中的虚线。gydF4y2Ba3.gydF4y2BaL的数值模拟结果与模拟结果吻合较好，从而覆盖了两个极端。gydF4y2Ba

大的波动gydF4y2Ba

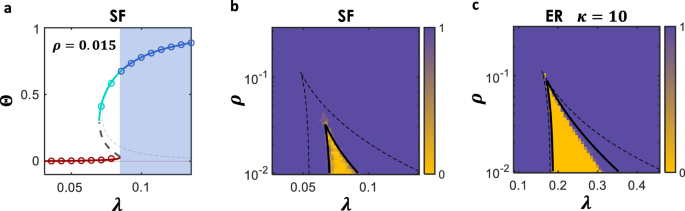
我们的MF理论面临的另一个挑战是大波动。这是当网络具有较小的平均度时，特别是对于表现出广泛度分布的无标度(SF)网络，这代表节点度的巨大变化。对于这些情况，虽然我们的MF方法定性地预测了过渡，但它在临界点的位置上有一些偏差。为了克服这种网络的挑战，我们退回到Eq. (gydF4y2Ba5gydF4y2Ba)，并使用顺序参数Θ， Eq. (gydF4y2Ba3.gydF4y2Ba)，以确定系统状态。该方法不假设一般参数gydF4y2BaβgydF4y2Ba=gydF4y2BaλgydF4y2BaκgydF4y2Ba，甚至不是全局参数gydF4y2BaκgydF4y2Ba．但分析和解决方案取决于gydF4y2BaλgydF4y2Ba在完全度分布上gydF4y2BapgydF4y2Ba_kgydF4y2Ba， Eq. (gydF4y2Ba5gydF4y2Ba)．在无花果。gydF4y2Ba4gydF4y2Ba时，我们提出该方法相对于上述方法的优点，用式(gydF4y2Ba8gydF4y2Ba)．数字gydF4y2Ba4gydF4y2Baa显示了模拟与理论之间很好的一致性，式(gydF4y2Ba5gydF4y2Ba)的无标度网络gydF4y2BaγgydF4y2Ba= 3.5和gydF4y2BakgydF4y2Ba_0gydF4y2Ba= 15。在无花果。gydF4y2Ba4gydF4y2BaB，我们提出(gydF4y2BaβgydF4y2Ba,gydF4y2BaρgydF4y2Ba)图中相同无标度网络的相位图。gydF4y2Ba4gydF4y2Baa.连续的线表示Eq. (gydF4y2Ba5gydF4y2Ba)，与模拟结果非常吻合，而虚线表示式(gydF4y2Ba8gydF4y2Ba)失败。SF的相图表明，与Erdős-Rényi (ER)相比，SF变得可持续的敏感性更高。例如，如图。gydF4y2Ba4gydF4y2BaC和b，gydF4y2BaρgydF4y2Ba_0gydF4y2Ba确保不存在不可持续阶段的ER约为0.1，而在SF中仅为0.03。SF网络较小gydF4y2BaγgydF4y2Ba，或更小gydF4y2BakgydF4y2Ba_0gydF4y2Ba，也显示了公式与理论的一些偏差。(gydF4y2Ba5gydF4y2Ba)，见图。gydF4y2BaS4gydF4y2Ba．最后，我们在图中显示。gydF4y2Ba4gydF4y2Bac在ER中也有一个不是很大的度，gydF4y2BaκgydF4y2Ba= 10, Eq. (gydF4y2Ba5gydF4y2Ba)的精度(全线)明显优于式(gydF4y2Ba8gydF4y2Ba)(虚线)。gydF4y2Ba

附加的例子gydF4y2Ba

接下来，我们考虑其他两种类型的动力学来展示细胞动力学中没有出现的方面，以及演示我们框架的一般性。gydF4y2Ba

神经动力学gydF4y2Ba

作为我们的第二个例子，我们考虑由图中给出的一组方程控制的神经元动力学。gydF4y2Ba5gydF4y2Baa，基于对Wilson-Cowan模型的修正gydF4y2Ba^{52gydF4y2Ba，gydF4y2Ba53gydF4y2Ba}，见补充说明gydF4y2Ba4gydF4y2Ba4.2节。从图中可以看出。gydF4y2Ba5gydF4y2BaB(细光线)时，系统自然呈现s型曲线，包括三个动态阶段。不活跃期为小gydF4y2BaβgydF4y2Ba在美国，只有国家存在gydF4y2BaxgydF4y2Ba_0gydF4y2Ba，所有活动都被抑制。高的区域gydF4y2BaβgydF4y2Ba，那里只存在gydF4y2BaxgydF4y2Ba_1gydF4y2Ba，其中的活动gydF4y2BaxgydF4y2Ba_我gydF4y2Ba都相对较高。因此，对于高gydF4y2BaβgydF4y2Ba在美国，该系统是“自然可持续的”。在这两个极端之间，系统的特点是gydF4y2Ba双稳态gydF4y2Ba相，其中两者gydF4y2BaxgydF4y2Ba_0gydF4y2Ba而且gydF4y2BaxgydF4y2Ba_1gydF4y2Ba具有潜在的稳定性，因此该地区的活跃状态是不可持续的。然而，控制了一小部分gydF4y2BaρgydF4y2Ba= 0.02，活动Δ = 15，创建一个新的s型曲线，具有更窄的双稳定区域(粗线和符号)。因此，创建了一个持续的窗口(蓝色阴影)，其中控制驱动系统可持续发展。在无花果。gydF4y2Ba5gydF4y2BaC，我们观察到，在(gydF4y2BaκgydF4y2Ba，gydF4y2BaλgydF4y2Ba)讨论,gydF4y2BaρgydF4y2Ba= 0.02，加上基因调控发现的三个阶段(图;gydF4y2Ba3.gydF4y2BaJ)，自然可持续阶段，系统在没有任何干预的情况下是可持续的。还要注意我们的理论，等式。（gydF4y2Ba8gydF4y2Ba)及(gydF4y2Ba11gydF4y2Ba)，预测所需gydF4y2BaλgydF4y2Ba_cgydF4y2Ba维持给定的系统gydF4y2BaρgydF4y2Ba高温度= 0.02(白线)。数字gydF4y2Ba5gydF4y2BaD显示(gydF4y2BaβgydF4y2Ba，gydF4y2BaρgydF4y2Ba)相位图gydF4y2BaκgydF4y2Ba= 20,60,100。gydF4y2Ba

旋转动力学gydF4y2Ba

作为我们的最后一个例子，我们探索了由铁磁相互作用连接的自旋动力学，由图中的方程捕获。gydF4y2Ba5gydF4y2Bae，基于Ising-Glauber模型gydF4y2Ba^54gydF4y2Ba．这个例子不同于上面的两个例子，因为这个动态中的相互作用是“吸引”的，而不是“确证的”。此外，相互作用完全对称地朝向两种稳定状态，而在上面的例子中，它们只朝向高活性状态。此外，方程的形式不包括在我们的框架中，Eq. (gydF4y2Ba1gydF4y2Ba)，然而，类似的分析也适用于这种动态，参见补充说明gydF4y2Ba4gydF4y2Ba4.3节。gydF4y2Ba

数字gydF4y2Ba5gydF4y2BaF表示自由系统相图的显著变化(细线)由于控制节点(粗线)与分数gydF4y2BaρgydF4y2Ba= 0.1有活动Δ = 1。与自由系统的对称状态(细线和轻线)相反，强制系统显示一个区域(蓝色阴影)gydF4y2BaxgydF4y2Ba_1gydF4y2Ba是可持续的。注意此区域为弱连通性(小gydF4y2BaβgydF4y2Ba)与上面的例子不同。这是相互作用吸引本质的结果，因为它引起了向上拉的受控节点和向下拉的自由节点之间的竞争。自由节点在数量上有优势，但是对于小节点来说gydF4y2BaβgydF4y2Ba，自然负解很小(绝对值)，对于足够大的Δ，强制节点获胜。在无花果。gydF4y2Ba5gydF4y2BaG，我们将相图显示在(gydF4y2BaκgydF4y2Ba，gydF4y2BaλgydF4y2Ba)空格。对于自旋动力学，由于对称吸引相互作用，单节点的可持续性相位不存在。原因是，当外部信号从源节点传播到邻居节点时，它们平均只有一个后面的邻居把它们拉起来，而不止一个邻居把它们拉下来。由于州与州之间的对称性，在数量上占优势。因此，即使干预力Δ很高，其影响也会随着距离的增加而衰减，并且只会在无限系统中产生局部影响。数字gydF4y2Ba5gydF4y2BaH表示(gydF4y2BaβgydF4y2Ba，gydF4y2BaρgydF4y2Ba)相图，与上面解释的例子相比，它具有不同的形状。还要注意，在这种情况下，没有临界点。gydF4y2Ba

在本文中，我们研究了在复杂网络中发生的动态是如何受到动态干预的影响的。尽管人们对复杂网络的结构已经有了非常广泛的认识，但关于复杂网络动力学演化的知识仍在不断地发现。我们研究的目标是通过控制一小部分节点来了解影响网络动态的方式。gydF4y2Ba

我们研究了对系统进行简单控制的效果，即强制部分节点，gydF4y2BaρgydF4y2Ba，有一个想要的活动，gydF4y2BaxgydF4y2Ba_我gydF4y2Ba=Δ。我们表明，这样简单的干预，即使很小gydF4y2BaρgydF4y2Ba并不是很大的Δ，可能会对系统的动态行为产生至关重要的影响。我们发现，控制部分节点，并不只是使系统的自然状态有所上升或下降，而是在一定条件下，消除了一些潜在的系统状态。我们证明，这种状态的消除可以将一个有效但不可持续的系统转变为可持续的系统。这是因为通过控制消除潜在的功能失调状态可以消除过渡到潜在的不活跃状态的危险。我们开发了一个通用框架，应用于三种动力学，(i)细胞动力学，(ii)神经元动力学和(iii)自旋动力学，揭示了受控系统的相图，通过它我们可以预测，例如，使系统可持续发展所需的最小节点比例。gydF4y2Ba

不同于复杂网络的“控制理论”gydF4y2Ba^29gydF4y2Ba，它探索了在某个连续体积内将系统移动到任何所需状态的能力，这里我们的目标根本不是移动系统，而是消除系统潜在的不希望的非活动状态，通过这种方式，系统保持在其自然稳定的活动状态，这是一个更容易的任务，允许我们进行分析分析。然而，我们的框架能够捕捉系统相图的全局变化，而复杂网络上的非线性动力学控制理论通常只提供局部信息gydF4y2Ba^29gydF4y2Ba而不是全球性的。gydF4y2Ba

我们对简单干预对网络动力学影响的基本和初步分析为未来的研究打开了大门。例如，人们可以探索其他更复杂和/或现实的干预措施，例如受控节点的非随机扩展，例如局部选择，或不同的控制，例如，向受控节点提供一些恒定或动态的通量，而不是像我们在这里考虑的那样仅仅迫使它们的活动保持恒定。gydF4y2Ba

这项工作的另一个自然推广是扩展式(gydF4y2Ba1gydF4y2Ba)，因为有各种各样的动态表现出不同的模式，例如，扩散相互作用，gydF4y2BaxgydF4y2Ba_jgydF4y2Ba−gydF4y2BaxgydF4y2Ba_我gydF4y2Ba，而不是Eq. (gydF4y2Ba1gydF4y2Ba)．gydF4y2Ba

还要注意，具有非常广泛的度分布的网络，例如指数低于3的无标度网络，或具有非常低的度的网络，挑战了我们理论的定量准确性，见图。gydF4y2Ba3.gydF4y2BaA代表低gydF4y2BaκgydF4y2Ba和无花果。gydF4y2BaS4gydF4y2BaSF与gydF4y2BaγgydF4y2Ba= 2.5。这些挑战需要进一步研究。gydF4y2Ba

最后，值得注意的是，控制一小部分节点可以维持一个非常大的网络。这有点类似于相互依赖网络渗透的静态结构问题，其中一小部分增强节点可以显著提高系统的鲁棒性gydF4y2Ba^55gydF4y2Ba．gydF4y2Ba

强制系统分析gydF4y2Ba

在本节中，我们将分析一个强制系统的状态。对于没有控制的自由系统的分析，请参见补充说明gydF4y2Ba1gydF4y2Ba．gydF4y2Ba

按照式中所示的控制的影响(gydF4y2Ba2gydF4y2Ba)，并测试它是否使系统可持续，我们分析Eq. (gydF4y2Ba2gydF4y2Ba)来发现系统在被迫时的状态。自由节点的动力学(gydF4y2Ba\(我在{{{{{{{\ \ mathcal {D }}}}}}}}\)gydF4y2Ba)，根据式(gydF4y2Ba2gydF4y2Ba),是gydF4y2Ba

通过把相邻的和分开gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba和邻居在一起gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba转向gydF4y2Ba

为了找到系统的稳态，我们要求弛豫，这样导数就消失了，gydF4y2Ba

在哪里gydF4y2Ba\ ({x} _{我}^ {*}\)gydF4y2Ba表示节点的松弛活动值gydF4y2Ba我gydF4y2Ba,gydF4y2Ba\ ({k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}\)gydF4y2Ba中邻居的个数gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba节点的gydF4y2Ba我gydF4y2Ba在gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba．安排条件，我们得到gydF4y2Ba

在哪里gydF4y2Ba

接下来，我们应用基于程度的平均场近似gydF4y2Ba^{42gydF4y2Ba，gydF4y2Ba48gydF4y2Ba，gydF4y2Ba49gydF4y2Ba，gydF4y2Ba50gydF4y2Ba，gydF4y2Ba51gydF4y2Ba}，替换二进制值，gydF4y2Ba一个gydF4y2Ba_{我gydF4y2BajgydF4y2Ba}的概率gydF4y2Ba\(我在{{{{{{{\ \ mathcal {D }}}}}}}}\)gydF4y2Ba而且gydF4y2Ba\ (j在{{{{{{{\ \ mathcal {D }}}}}}}}\)gydF4y2Ba以他们的学历来联系，也就是说gydF4y2Ba\ ({k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}{ k} _ {j }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}/(| {{{{{{{\ mathcal {D }}}}}}}}| \ langle {k }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\ 纠正)\)gydF4y2Ba由于配置模型的结构。这给了gydF4y2Ba

注意，现在求和不依赖于gydF4y2Ba我gydF4y2Ba，因此我们可以写gydF4y2Ba

通过定义顺序参数，gydF4y2Ba

一个节点的平均影响是什么gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba(自由节点)在一个节点上gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba．用方程式。（gydF4y2Ba21gydF4y2Ba)及(gydF4y2Ba22gydF4y2Ba)，我们得到了阶参数Θ的一个自洽方程，gydF4y2Ba

即Eq. (gydF4y2Ba5gydF4y2Ba)以上。为了解这个方程，我们应该替换中节点的和gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba通过一些理论上可计算的项，无需测量节点度。因此，我们通过写出Eq. (gydF4y2Ba23gydF4y2Ba),gydF4y2Ba

对所有可能性取平均值gydF4y2Ba\ ({k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\)gydF4y2Ba而且gydF4y2Ba\ ({k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}\)gydF4y2Ba，它得到了形式gydF4y2Ba

在哪里gydF4y2Ba\ \公关({k} _ {j }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}= k, k {} _ {j }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}={ k} ^ {{\ '}}) \)gydF4y2Ba联合概率是那个节点吗gydF4y2Ba\ (j在{{{{{{{\ \ mathcal {D }}}}}}}}\)gydF4y2Ba有gydF4y2BakgydF4y2Ba邻居gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba(空闲节点)和gydF4y2Ba\ ({k} ^ {{\ '}} \)gydF4y2Ba邻居gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba(强制节点)。这个联合概率是由度分布决定的gydF4y2BapgydF4y2Ba_kgydF4y2Ba以及强制节点的选择方式(gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba)．其次，不要跑过去gydF4y2Ba\ (k, k {} ^ {{\ '}}) \)gydF4y2Ba(gydF4y2Ba\ ({k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\)gydF4y2Ba而且gydF4y2Ba\ ({k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}\)gydF4y2Ba分别)，我们跑过(gydF4y2BakgydF4y2Ba_0gydF4y2Ba,gydF4y2BakgydF4y2Ba)在这里gydF4y2Ba\ ({k} _ {0} = {k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {V }}}}}}}}}\)gydF4y2Ba自由度是一个结点，在哪里gydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba是所有节点的集合，和gydF4y2Ba\ (k = {k }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\)gydF4y2Ba空闲节点的空闲邻居数。当然，对于每个节点gydF4y2Ba\ ({k} ^ {{\ '}} = {k} _ {0} - k \)gydF4y2Ba也就是说gydF4y2Ba\ ({k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}={ k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {V }}}}}}}}}-{ k} _{我 }^{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\)gydF4y2Ba．执行此索引更改，我们获得gydF4y2Ba

并将Pr(gydF4y2BakgydF4y2Ba，gydF4y2BakgydF4y2Ba_0gydF4y2Ba) = Pr(gydF4y2BakgydF4y2Ba_0gydF4y2Ba)公关(gydF4y2BakgydF4y2Ba∣gydF4y2BakgydF4y2Ba_0gydF4y2Ba)的收益率gydF4y2Ba

条款gydF4y2Ba\ (\ langle {k }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\ 纠正\)gydF4y2Ba公关(gydF4y2BakgydF4y2Ba_0gydF4y2Ba)和Pr(gydF4y2BakgydF4y2Ba∣gydF4y2BakgydF4y2Ba_0gydF4y2Ba)除度分布外，还取决于强制节点的选择方式gydF4y2BapgydF4y2Ba_kgydF4y2Ba．现在，我们考虑控制节点的完全随机选择。在这种情况下，gydF4y2Ba\ \(公关({k} _ {0}) = {p} _ {{k} _ {0}} \)gydF4y2Ba(网络的度分布)因为gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba是随机的，因此有相同的度分布gydF4y2BapgydF4y2Ba_kgydF4y2Ba作为整个网络gydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba．邻居在的概率gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba是gydF4y2BaρgydF4y2Ba,从而gydF4y2Ba\ (\ langle {k }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\ 纠正= \ langle {k }_{{{{{{{{\ mathcal {V}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\ 纠正= \ langle k \纠正(1 - \ρ)\)gydF4y2Ba作为二项分布的平均值，和gydF4y2Ba\ \(公关(k | {k} _{0}) = \离开({{k} _{0} \在{k}} \右){(1 - \ρ)}^ {k}{\ρ}^ {{k} _ {0} - k} \)gydF4y2Ba，二项分布。代入这些，我们最终得到，对于随机选择的受控节点，gydF4y2Ba

在哪里gydF4y2Ba\ (p {} _ {{k} _ {0}} \)gydF4y2Ba为度分布，kgydF4y2Ba>是平均度。根据度分布，该自洽方程在理论上是可解的。我们用Eq (gydF4y2Ba28gydF4y2Ba)绘制图中的理论线。gydF4y2Ba4gydF4y2Ba．gydF4y2Ba

小波动MFgydF4y2Ba

为了得到一个更简单和信息丰富的方程，我们应用了另一种平均场(MF)近似gydF4y2Ba^25gydF4y2Ba该方法适用于小波动，如图所示。gydF4y2Ba3.gydF4y2Ba5gydF4y2Ba．根据这个MF，我们将平均值插入Eq. (gydF4y2Ba22gydF4y2Ba)进入函数gydF4y2Ba米gydF4y2Ba_2gydF4y2Ba（gydF4y2BaxgydF4y2Ba)，以获取gydF4y2Ba

其中，非受迫节点的平均活动，gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba，定义为gydF4y2Ba

对式求平均值(gydF4y2Ba21gydF4y2Ba)，利用MF近似，我们得到gydF4y2Ba

在哪里gydF4y2Ba

平均学位是多少gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba到gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba节点分别通过链接内接近gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba．代入Eq. (gydF4y2Ba29gydF4y2Ba)代入Eq. (gydF4y2Ba31gydF4y2Ba)，得到一个受迫系统活度的方程，gydF4y2Ba

的数量gydF4y2Ba\({\卡帕 }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}\)gydF4y2Ba而且gydF4y2Ba\({\卡帕 }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {F }}}}}}}}}\)gydF4y2Ba当然取决于选择集合的方式gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba控制节点。现在，为了简单起见，我们假设gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba是完全随机选择的，然后求出这种情况下的这些量。补充说明gydF4y2Ba2gydF4y2Ba我们分析一般情况。gydF4y2Ba

随机选择gydF4y2Ba

选择受控节点集gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba随机确定被控制节点的度分布，gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba，自由节点gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba，以及所有的节点gydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba，都是一样的，gydF4y2BapgydF4y2Ba_kgydF4y2Ba．这使我们能够分析式(gydF4y2Ba32gydF4y2Ba)，出现在式(gydF4y2Ba33gydF4y2Ba)，因为我们可以替换网络子集上的平均值(gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba或gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba)以整个网络的平均值计算gydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba．考虑任意的节点gydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba属于gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}}\)gydF4y2Ba与可能性gydF4y2BaρgydF4y2Ba，我们利用瓦尔德的身份，gydF4y2Ba

在第二个时刻gydF4y2Ba\ (\ langle {k }_{{{{{{{{\ mathcal {D}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}^{ 2} \纠正\)gydF4y2Ba时，我们首先将平均值改为ongydF4y2Ba\({{{{{{{\ mathcal {V }}}}}}}}\)gydF4y2Ba，gydF4y2Ba\ (\ langle {k }_{{{{{{{{\ mathcal {V}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}^{ 2} \纠正\)gydF4y2Ba．然后我们定义一个变量gydF4y2BaygydF4y2Ba_jgydF4y2Ba哪个是邻居数的指标gydF4y2BajgydF4y2Ba的gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba，以致于gydF4y2BaygydF4y2Ba_jgydF4y2Ba= 1 if邻居gydF4y2BajgydF4y2Ba属于gydF4y2Ba\({{{{{{{\ mathcal {D }}}}}}}}\)gydF4y2Ba而且gydF4y2BaygydF4y2Ba_jgydF4y2Ba否则= 0。因此,gydF4y2Ba\ ({k }_{{{{{{{{\ mathcal {V}}}}}}}} \ {{{{{{{\ mathcal {D }}}}}}}}}=\ mathop{总和\}\ nolimits_ {j = 1} ^ {k} {y} _ {j} \)gydF4y2Ba其中索引gydF4y2BajgydF4y2Ba在任意节点的邻居上运行。随机变量gydF4y2BaygydF4y2Ba_jgydF4y2Ba是独立的，且均值为1−gydF4y2BaρgydF4y2Ba因此,gydF4y2Ba

代入方程式。（gydF4y2Ba34gydF4y2Ba)及(gydF4y2Ba35gydF4y2Ba式(gydF4y2Ba32gydF4y2Ba)提供gydF4y2Ba

这个结果是非常直观的，因为这个量代表了一个自由节点通过一个自由节点接近的自由邻居的预期数量。因此，它肯定有一个自由邻居，由于任意邻居的平均度是gydF4y2BaκgydF4y2Ba，它已经gydF4y2BaκgydF4y2Ba−多出1个邻居，但只是一小部分gydF4y2BaρgydF4y2Ba他们中的任何一个都将被控制。gydF4y2Ba

接下来，我们开始计算Eq. (gydF4y2Ba32gydF4y2Ba)．gydF4y2Ba

我们已经找到了Eq的第二项(gydF4y2Ba35gydF4y2Ba)．第一项是gydF4y2Ba

堵塞方程式。（gydF4y2Ba35gydF4y2Ba)及(gydF4y2Ba38gydF4y2Ba)代入Eq. (gydF4y2Ba37gydF4y2Ba)给gydF4y2Ba

代入方程式。（gydF4y2Ba34gydF4y2Ba)及(gydF4y2Ba39gydF4y2Ba)代入Eq. (gydF4y2Ba32gydF4y2Ba)我们得到gydF4y2Ba

这个公式也很直观，因为它表示一个自由节点通过另一个自由节点接近的强制邻居的数量。gydF4y2BaκgydF4y2Ba是期望的程度，而剩下的呢gydF4y2BaκgydF4y2Ba−1个邻居，分数gydF4y2BaρgydF4y2Ba预计是被迫的。gydF4y2Ba

代入方程式。（gydF4y2Ba36gydF4y2Ba)及(gydF4y2Ba40gydF4y2Ba)代入Eq. (gydF4y2Ba33gydF4y2Ba)，我们得到随机选择受控节点的强制系统的均场方程，gydF4y2Ba

求极限gydF4y2BaκgydF4y2Ba≫gydF4y2Ba1、回忆gydF4y2BaβgydF4y2Ba=gydF4y2BaλgydF4y2BaκgydF4y2Ba时，这个方程是这样的gydF4y2Ba

隔离gydF4y2BaβgydF4y2Ba时，得到Eq. (gydF4y2Ba8gydF4y2Ba)以上,gydF4y2Ba

哪个产生了之间的关系gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba而且gydF4y2BaβgydF4y2Ba，确定所捕获的每个拓扑的强制系统的平均活动gydF4y2BaβgydF4y2Ba．此外，系统状态取决于干预特征，gydF4y2BaρgydF4y2BaΔ。注意替换gydF4y2BaρgydF4y2Ba式中= 0 (gydF4y2Ba43gydF4y2Ba)恢复系统空闲的情况，请参见补充说明gydF4y2Ba1gydF4y2Ba．认识到一个受迫系统的稳态(gydF4y2BaρgydF4y2Ba> 0)与自由系统(gydF4y2BaρgydF4y2Ba= 0)时，我们可以通过保留部分节点来回答维持系统的主要问题。在下一节中，我们发现细胞动力学的持续窗口，即由于外部控制，一个不可持续的网络变得可持续的区域。gydF4y2Ba

维持细胞动力学gydF4y2Ba

迫使系统gydF4y2Ba

为了检验细胞动力学的行为(gydF4y2Ba9gydF4y2Ba)在持续条件下，我们寻求根据式(gydF4y2Ba43gydF4y2Ba)，gydF4y2Ba

该公式生成了一个新的强制系统相图，如图所示。gydF4y2Ba3.gydF4y2BaD(粗曲线)为gydF4y2BaρgydF4y2Ba= 0.03和Δ = 5，显示了一个s形图，现在也有一个新的活动区域(蓝色阴影)，其中只有gydF4y2BaxgydF4y2Ba_1gydF4y2Ba的存在。这种制度被认为是可持续的阶段。值得注意的是，仿真结果(符号)与理论吻合良好。模拟的是ER网络gydF4y2BaκgydF4y2Ba= 40和gydF4y2BaNgydF4y2Ba= 10gydF4y2Ba^4gydF4y2Ba．的价值gydF4y2BaλgydF4y2Ba各不相同。gydF4y2Ba

维护窗口gydF4y2Ba

寻找gydF4y2BaβgydF4y2Ba_cgydF4y2Ba时，则受迫系统为可持续的，根据式(gydF4y2Ba11gydF4y2Ba)的导数gydF4y2BaβgydF4y2Ba式中(gydF4y2Ba44gydF4y2Ba)关于gydF4y2Ba酒吧\ (\ {{{{{{{{\ bf {x }}}}}}}}}\)gydF4y2Ba为零，如Eq. (gydF4y2Ba11gydF4y2Ba)要求，让步gydF4y2Ba

表示gydF4y2Ba酒吧\ (u = 1 + {\ {{{{{{{{\ bf {x }}}}}}}}}}^{- h} \)gydF4y2Ba，我们得到，gydF4y2Ba

排列项得到一个可解的二次方程，gydF4y2Ba

谁给出的解gydF4y2Ba

取较小的解gydF4y2Ba酒吧\ ({\ {{{{{{{{\ bf {x }}}}}}}}}}_{ c} \)gydF4y2Ba向可持续制度的过渡(见图。gydF4y2Ba3.gydF4y2BaD)，我们得到gydF4y2Ba

代入式(gydF4y2Ba44gydF4y2Ba)提供gydF4y2BaβgydF4y2Ba_cgydF4y2Ba（gydF4y2BaρgydF4y2Ba， Δ)，会得到一个复杂的表达式。然而，让我们在“小”的限制下展开它gydF4y2BaρgydF4y2Ba而且，结果很小gydF4y2Ba酒吧\ ({\ {{{{{{{{\ bf {x }}}}}}}}}}_{ c} \)gydF4y2Ba如图所示。gydF4y2Ba3.gydF4y2BaD，得到的比例gydF4y2BaβgydF4y2Ba_cgydF4y2Ba而且gydF4y2BaρgydF4y2Ba在小的限度里gydF4y2BaρgydF4y2Ba．为此，我们回到Eq. (gydF4y2Ba45gydF4y2Ba)，以取得先导命令gydF4y2Ba

代入式(gydF4y2Ba44gydF4y2Ba)，我们终于得到了gydF4y2Ba

谁提供连接之间的伸缩gydF4y2BaβgydF4y2Ba和对照组的分数gydF4y2BaρgydF4y2Ba在从不可持续阶段过渡到可持续阶段的小gydF4y2BaρgydF4y2Ba在细胞动力学中。反比关系给出了给定的gydF4y2BaβgydF4y2Ba临界所需分数gydF4y2BaρgydF4y2Ba_cgydF4y2Ba为了维持一个网络，gydF4y2Ba

在无花果。gydF4y2Ba3.gydF4y2BaK，我们给出了gydF4y2Ba一个gydF4y2Ba= 1,gydF4y2BahgydF4y2Ba= 2，因此我们观察到缩放gydF4y2BaρgydF4y2Ba_cgydF4y2Ba~gydF4y2BaβgydF4y2Ba^{−2gydF4y2Ba}= (gydF4y2BaλgydF4y2BaκgydF4y2Ba）gydF4y2Ba^{−2gydF4y2Ba}．在无花果。gydF4y2BaS3gydF4y2Ba的不同值，我们也显示了结果gydF4y2Ba一个gydF4y2Ba，gydF4y2BahgydF4y2Ba得到了不同的指数，模拟结果与理论吻合较好。gydF4y2Ba

请注意，正如我们在补充说明中详细讨论的那样gydF4y2Ba3.gydF4y2Ba，限度小gydF4y2BaρgydF4y2Ba和小kgydF4y2Ba>挑战我们的平均场，它提供了(gydF4y2Ba52gydF4y2Ba)，只适用于小型gydF4y2BaρgydF4y2Ba．因此，即使模拟结果在图。gydF4y2Ba3.gydF4y2Bak表示预测指数，因为度较大，相反，图中的结果。gydF4y2Ba3.gydF4y2Bal显示了与预测缩放的偏差，因为MF假设由于小而被打破gydF4y2BaρgydF4y2Ba平均度也很小。gydF4y2Ba

三重临界点gydF4y2Ba

超过某一点(gydF4y2BaβgydF4y2Ba_0gydF4y2Ba，gydF4y2BaρgydF4y2Ba_0gydF4y2Ba)时，不可持续阶段消失，高活性态与低活性态之间的过渡变为连续，如图所示。gydF4y2Ba3.gydF4y2Bae, g, h。当不可持续区域边缘的两个过渡点合并时，就会发生这种情况。为了实现这一点，Eq.(应该只有一个解。gydF4y2Ba46gydF4y2Ba)，因此平方根内的项必须等于零。因此我们要求gydF4y2Ba

屈服gydF4y2Ba

的临界值是多少gydF4y2BaρgydF4y2Ba超过这个值，系统就完全可持续了因为双稳定机制消失了。把这个代入方程。（gydF4y2Ba49gydF4y2Ba)及(gydF4y2Ba44gydF4y2Ba)提供的值gydF4y2BaβgydF4y2Ba_cgydF4y2Ba临界点的。gydF4y2Ba

在图的模拟中。gydF4y2Ba3.gydF4y2Ba我们设置gydF4y2Ba一个gydF4y2Ba= 1,gydF4y2BahgydF4y2Ba= 2，得到gydF4y2BaρgydF4y2Ba_0gydF4y2Ba= 1/(1 + 8/(1 + Δ .gydF4y2Ba^{−gydF4y2BahgydF4y2Ba}))，并设置Δ = 5给出gydF4y2BaρgydF4y2Ba_0gydF4y2Ba≈1/9，而使用Δ = 1得到gydF4y2BaρgydF4y2Ba_0gydF4y2Ba= 1/5。一般来说，对于高Δ，我们得到gydF4y2BaρgydF4y2Ba_0gydF4y2Ba≈(gydF4y2BahgydF4y2Ba−gydF4y2Ba一个gydF4y2Ba）gydF4y2Ba^2gydF4y2Ba／（gydF4y2BahgydF4y2Ba+gydF4y2Ba一个gydF4y2Ba）gydF4y2Ba^2gydF4y2Ba．gydF4y2Ba